Растяжение с изгибом

Рассмотрим растяжение с изгибом (см.рис.19.3).

рис.19.3 рис.19.4

Проанализируем задачу отыскания нормального напряжения .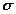

Ясно, что он складывается из напряжений, возникающих при растяжении ( 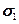), при вертикальном изгибе ( ), горизонтальном изгибе ( ), т.е.:

Здесь

, , .

Суммируя, получаем:

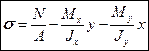(19.1)

Эту формулу иногда называют основной формулой сопромата.

Здесь - это координаты точки (бесконечно малой площадки), в которой мы вычисляем .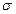

рис.19.5

Ясно, что из (19.1) следует ряд формул для простых деформаций:

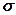1) Если нет изгиба, то . Тогда получим для простого растяжения: .

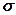2) Если нет растяжения, но то получим для косого изгиба:

.

3) Если 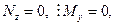то получим случай прямого поперечного изгиба:

.