Угол закрутки тонкостенных стержней замкнутого профиля

Рассмотрим поворот сечения на угол 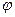- угол поворота правого торца относительно левого (рис.18.26). При этом точка 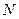перейдет в точку .

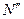Из рисунка видно, что:

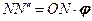. (18.20)

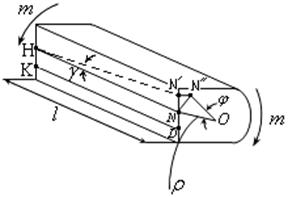
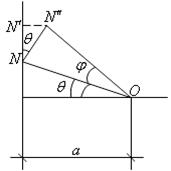
рис.18.26 рис.18.27

Как и в случае круглых стержней выразим теперь 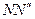через угол 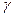- угол сдвига прямоугольника HNLK. Как видно из рисунка

.

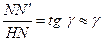Здесь 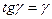в силу малости 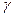. Тогда

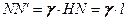. (18.21)

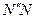Выразим далее через . Используя равенство углов с перпендикулярными сторонами, получим, что 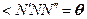. Тогда:

.

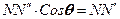Подстановка сюда соотношений (18.20), (18.21)дает:

. (18.22)

По закону Гука

.

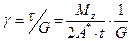Из (18.22) с учетом формулы Бредта (18.19) получим:

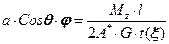. (18.23)

Отсюда вытекает, что якобы 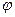зависит от 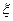. Для осреднения угла поворота разных точек контура используют следующий подход. В (18.23) слева и справа у нас одинаковые функции. Значит и интегралы от них будут одинаковы:

.

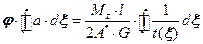Ранее было получено, что слева интеграл равен (см.формулу (18.18)). Тогда: .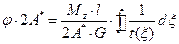

Таким образом, получаем, следующую формулу Бредта для угла :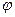

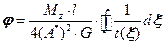. (18.24)

Здесь интеграл называется относительным периметром стенки трубы:

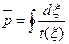. (18.25)

В компактной форме формулу Бредта для угла 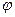запишем теперь в виде:

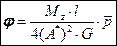(18.24)

Рассмотрим частные случаи.

1. Пусть .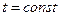

Тогда: ,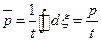

где р - периметр контура сечения трубы.

2. Пусть труба составлена из кусков с постоянными толщинами (см. рис.18.28) :

рис.18.28

Тогда: 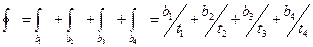(18.26)

Таким образом:

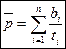(18.27)