Закон Ома для неоднородного участка цепи. Закон Ома для замкнутого контура.

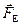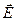Вернёмся ещё раз к рис. 7.1. Здесь изображена замкнутая проводящая цепь. На участке цепи 1-а-2 движение носителей заряда происходит под действием только электростатической силы = q . Такие участки называются однородными.

Совсем по-другому обстоят дела на участке контура 2-b-1. Здесь на заряды действует не только электростатическая, но и сторонняя сила. Полную силу найдем, сложив эти две:

.

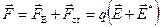Участок замкнутого контура, где наряду с электростатической силой действуют и сторонние силы, называют неоднородным.

Можно показать, что на однородном участке цепи средняя скорость направленного движения носителей заряда пропорциональна действующей на них силе. Для этого достаточно сравнить формулы, полученные на прошлой лекции: 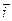= 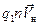(6.3) и 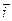= l 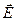(6.13).

Пропорциональность скорости силе, а плотности тока — напряжённости сохранится и в случае неоднородного участка цепи. Но теперь напряжённость поля равна сумме напряжённостей электростатического поля 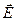и поля сторонних сил :

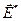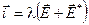. (7.5)

Это уравнение закона Ома в локальной дифференциальной форме для неоднородного участка цепи.

Теперь перейдём к закону Ома для неоднородного участка цепи в интегральной форме.

Выделим двумя близкими сечениями DS участок dl трубки тока (рис. 7.3.). Сопротивление этого участка:

,

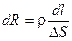а плотность тока можно связать с силой тока:

.

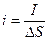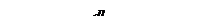
Рис. 7.3.

Эти два выражения используем в уравнении (7.5), спроецировав его предварительно на линию тока:

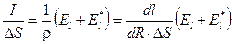
Проинтегрировав последнее уравнение по неоднородному участку 1-2, получим:

.

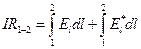Произведение IR_1-2 = U — напряжение на участке 1-2;

первый интеграл справа 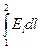= = 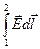j₁ – j₂ — разность потенциалов на концах участка;

второй интеграл 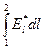= = 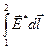e_1-2 — э.д.с. источника тока.

Учтя всё это, конечный результат запишем в виде:

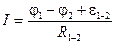. (7.6)

Это закон Ома для неоднородного участка цепи в интегральной форме. Обратите внимание, что напряжение на неоднородном участке цепи U не совпадает с разностью потенциалов на его концах (j₁ – j₂):

IR_1-2 = U_1-2 = (j₁ – j₂) + e_1-2. (7.7)

Эти две величины равны только в случае однородного участка, где источники тока отсутствуют и e_1-2 = 0. Тогда:

U_1-2 = j₁ – j₂.

Для замкнутого контура уравнение закона Ома (7.6) несколько видоизменяется, так как разность потенциалов в этом случае равна нулю:

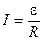. (7.8)

В законе Ома для замкнутой цепи (7.8) R — полное сопротивление контура, складывающееся из внешнего сопротивления цепи R₀ и внутреннего сопротивления источника r:

R = R₀ + r.