Третий закон Ньютона. Характер взаимодействий между материальными точками (телами) определяется третьим законом Ньютона:всякое действие материальных точек (тел) друг на друга носит

Характер взаимодействий между материальными точками (телами) определяется третьим законом Ньютона:всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:

. (10)

Рассмотрим, например, два разноименных заряженных тела массам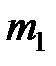и и 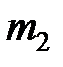, которые притягивают друг друга. Под действием сил 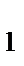F и F 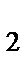тела приобретают ускорения а и а .

Согласно второму закону Ньютона можно записать:

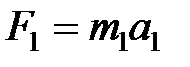и 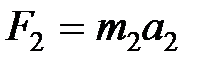. (11)

Используя выражения (10) и (11), получим

,

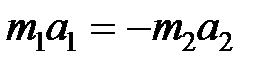или

т.е. ускорения двух взаимодействующих тел обратно пропорциональны их массам и направлены в противоположные стороны.

1. Упругие силы, закон Гука.

Все твердые тела способны под действием внешних сил деформироваться, т. е. изменять свою форму или объем.

Тела, в которых после прекращения действия внешних сил деформация полностью исчезает и первоначальная форма тела и его объем полностью восстанавливаются, называют абсолютно упругими, а саму деформацию — упругой. Тела, которые после прекращения действия внешних сил не восстанавливают свою первоначальную форму (и объем), называют неупругими или пластичными; соответственно их деформацию называют неуп­ругой, пластичной. В случае, когда после устранения внешних сил деформация полностью сохраняется, тело называют абсо­лютно неупругим.

Свойство тел восстанавливать форму и объем после прекращения действия внешних сил называют упругостью. Различают объемную упругость и упругость формы. Объемная упругость — универсальное свойство всех тел, включая жидкости и газы .

Внутренние силы, возникающие в упругих телах при небольших деформациях, называют упругими. Их нам и предстоит изучить. Внутренние силы в неупругих телах относятся к силам иного вида, называемым силами вязкости или силами внутреннего трения. Эти силы мы изучим позднее.

Виды упругих деформаций. Существует множество различных видов упругих деформаций: одностороннее растяжение (и сжатие), всестороннее растяжение (и сжатие), изгиб, сдвиг, кручение и др.

Закон Гука. При любой деформации (простой или сложной) в теле возникают упругие силы. Р. Гук еще в 1675г. обнаружил, что величина и направление сил упругости определенным образом зависят как от вида, так и от величины деформации.

Установленный Гуком закон, носящий теперь его имя, состоит в следующем:

а) при любой малой деформации сила упругости пропорциональна величине деформации;

б) малые деформации тела пропорциональны приложенным силам.

Чтобы записать этот закон в математической форме, нужно ввести новые физические величины, характеризующие с количественной стороны деформацию и силу упругости.

Характеристики деформации.Деформация одно­стороннего растяжения возникает, например, в тонком стержне, один конец которого закреплен, а к другому приложена внешняя сила F, стремящаяся растянуть стержень (рис.3.3). Под действием приложенной силы стержень удлинится на величину 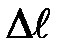, но после снятия нагрузки (если удлинение не превзошло определенного предела) возвращается к первоначальной длине. Количественной характеристикой деформации может служить абсолютное удлинение 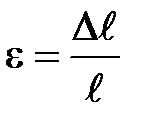, называемое также в общем виде относительной деформацией.

Относительное удлинение — отвлеченное число, указывающее, на какую часть увеличилась или уменьши­лась первоначальная длина стержня. Величину 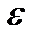можно рассматривать как удлинение, которое испытывает каждый участок стержня длиной 1 м (или 1 см). Замечательно то, что если весь стержень имеет относительное удлинение 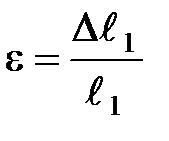, то при однородной деформации каждый элемент тела про­извольной длины 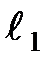имеет точно такое же относительное удлинение - (рис. 1).

l   F1 F2   l+Dl   Рис.

Таким образом, есть количественная характеристика деформации как в отношении всего стержня, так и в отношении его любой части, т. е. является исчерпывающей характеристикой однородной деформации данного вида.

Сила упругости F_упр, возникающая в растянутом стержне, оценивается по внешней растягивающей силе F. Из условия равновесия стержня имеем:

F_упр=-F. (12)

Но силы упругости F_упр действуют в любом сечении стержня (рис.1) и при однородной статистической деформации они повсюду одинаковы и равны растягивающей силе.

Нагружая нижний конец стержня гирями и измеряя при каждом грузе абсолютное удлинение, можно установить, что абсолютное удлинение прямо пропорционально длине стержня 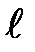, растягивающей силе F и обратно пропорционально поперечному сечению стержня S:

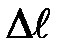= (13)

Переходя от пропорциональной зависимости к равенству, мы должны ввести коэффициент пропорциональности :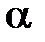

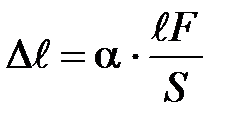(14)

Как показывает опыт, коэффициент 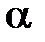зависит от рода материала, из которого сделан образец, и является, таким образом, характеристикой упругих свойств данного материала по отношению к деформации растяжения (и сжатия). Его называюткоэффициентом упругости.

Численное значение этого коэффициента определяют из опыта. Вводя в (14) модуль Юнга

Е=1/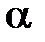

и заменяя F на F_упр, получим искомую зависимость силы уп­ругости от абсолютной деформации:

F_упр = 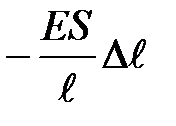, или F_упр =-k× 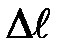. (15)

Полученное соотношение представляет собой одну из математических записей закона Гука для деформации растяжения. Знак минус в формуле (15) указывает, что направление силы упругости Fупр противоположно направлению растяжения.

Мы видим, что сила упругости, возникающая в теле при одностороннем растяжении (сжатии), прямо пропорциональна абсолютному удлинению тела. Коэффициент пропорциональности для данного тела зависит от его размеров ( 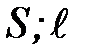) и модуля упругости материала Е. Величину k называют коэффициентом силы упругости или просто упругостью (для пружины - жесткостью).

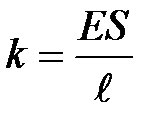(16)