Токи, ограниченные пространственным зарядом
11.1 Закон «трех вторых»
Рассмотрим закономерности прохождения потоков заряженных частиц (электронов или ионов) между электродами простейшей двухэлектродной вакуумной системы: эмиттерколлектор (катод-анод).
Состояния заряженных частиц в какой-либо системе определяются их взаимодействиями. При движении заряженных частиц в вакууме такими взаимодействиями являются, во-первых, кулоновские взаимодействия их друг с другом и, во-вторых, взаимодействия их с внешними электрическими или магнитными полями. Специфические квантовомеханические взаимодействия, например, учитываемые принципом Паули, практически никакой роли не играют из-за малых концентраций частиц в межэлектродном пространстве диода. Волновые свойства частиц здесь также можно не учитывать, так как изменения потенциалов в полях, имеющих место в межэлектродных промежутках на отрезках протяженностью в длину дебройлевской волны, очень малы.
В первую очередь, рассмотрение закономерностей движения заряженных частиц мы проведем на примере термоэлектронов. Однако все полученные выводы будут применимы и к анализу движения ионов с тепловыми начальными скоростями. В последнем случае вследствие значительно большей массы ионов по сравнению с массой электронов при тех же полях в межэлектродном пространстве скорость движения ионов значительно меньше, а поэтому объемная плотность заряда при равных плотностях электронного и ионного тока значительно больше в случае ионов, чем в случае электронов.
Начнем с рассмотрения качественной картины движения электронов. Предположим вначале для простоты, что система состоит из электрически соединенных плоских эмиттера (катода) и коллектора (анода). Направим ось х перпендикулярно к плоскостям катода и анода, а оси у и z параллельно им и поместим начало координат в плоскости катода. Расстояние между катодом и анодом обозначим через d. Пусть протяженность электродов в направлении осей у и z много больше d. Ясно, что все физические величины для этого случая зависят только от одной переменной х,т. е. рассматривается одномерная задача.
Распределение по составляющей vx0 начальной скорости вдоль оси х для термоэлектронов подчиняется закону Максвелла:
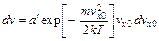 , (11.1)
, (11.1)
где dv количество электронов, проходящих через единицу поверхности катода, с составляющей скорости по оси х,лежащей в интервале от vx0до vx0 + dvx0; а' постоянная, т масса электрона, k постоянная Больцмана, Т абсолютная температура. Обозначим часть начальной кинетической энергии, связанную с компонентой скорости по оси х,через Wx0:
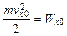 . (11.2)
. (11.2)
Тогда из (11.1) имеем
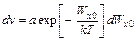 , (11.3)
, (11.3)
где а константа, равная а'/т. Из (11.3) легко получить среднее значение величины Wx0в потоке:
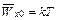 (11.4)
(11.4)
Например, при Т = 1000°К 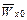 =0,085 эв,т. е.
=0,085 эв,т. е. 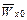 малы и составляют сотые или десятые доли эв. Это позволит в дальнейшем при приближенном рассмотрении задачи положить Wx0=0.
малы и составляют сотые или десятые доли эв. Это позволит в дальнейшем при приближенном рассмотрении задачи положить Wx0=0.
В случае электронов будем отсчитывать потенциалы от потенциала катода. Тогда наружная разность потенциалов Vнпросто будет равна анодному потенциалу VА. Положим, что внешняя разность потенциалов Vн= VAтакова, что внутренняя разность потенциалов Vвравна нулю (но ток, протекающий через диод, не равен, вообще говоря, нулю). В этом разделе током с анода мы будем пренебрегать. Объемный заряд индуцирует на катоде и на аноде положительные поверхностные заряды с равными плотностями sоК и sоА, на которых начинаются силовые линии электрического поля, создаваемого в межэлектродном пространстве движущимися электронами. Так как эти силовые линии кончаются на отрицательных зарядах в разных точках объема, густота силовых линий, а следовательно, и абсолютная величина напряженности электрического поля 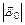 наибольшими будут у катода и анода. При этом
наибольшими будут у катода и анода. При этом 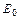 (0) > 0, тогда как
(0) > 0, тогда как 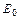 (d)< 0. Так как E(х) непрерывная функция, она проходит через нуль при некотором значении х = хт. Но тогда при х = хт имеется минимум потенциала V(хт)= Vm, а у потенциальной энергии электрона eV(x) максимум.
(d)< 0. Так как E(х) непрерывная функция, она проходит через нуль при некотором значении х = хт. Но тогда при х = хт имеется минимум потенциала V(хт)= Vm, а у потенциальной энергии электрона eV(x) максимум.
Таким образом, электроны, движущиеся в межэлектродном пространстве, создают потенциальный барьер, который со своей стороны влияет на их движение. Очевидно, что если у эмитируемого электрона Wx0< eVm,то такой электрон не сможет преодолеть этот барьер. При Wx0> eVm электрон преодолеет задерживающее поле и достигнет анода. Таким образом, лишь часть электронов, эмитируемых катодом, достигнет анода. Обозначим плотность этого тока, протекающего через диод, j, а плотность тока, соответствующего прохождению через диод всех термоэлектронов эмитируемых катодом, через js (сокращенно будем называть j током диода, a js током насыщения или током эмиссии катода). При Vв=0имеем j < js. Отметим, что наличие минимума потенциала в промежутке катод анод является характерным свойством поля объемного заряда r(x); оно сохраняется и при Vв¹0. В случае Vв¹0 напряженность E(х)и потенциал V(x)электрического поля в межэлектродном пространстве складываются из напряженности Er(х)и потенциала Vr(х)поля объемных зарядов и напряженности 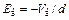 и потенциала
и потенциала 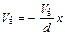 поля внутренней разности потенциалов, т. е.:
поля внутренней разности потенциалов, т. е.:
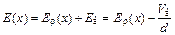 , (11.5)
, (11.5)
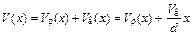 . (11.6)
. (11.6)
Для каждого значения Vвустановится свое поле объемных зарядов Vr(х). Если Eв < 0, то знаки Erи Eв у катода противоположны, тогда как у анода одинаковы. Поэтому даже в случае поля Eв,ускоряющего электроны от катода к аноду, напряженность результирующего поля у катода E(0) может быть отрицательна, равна нулю или положительна. Рассмотрим режимы работы диода во всех этих трех случаях.
1) E (0) < 0 и, следовательно, учитывая (11.5), Er(0) < 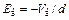 . Так как
. Так как 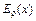 наибольшая у катода, то во всем межэлектродном пространстве E(х) < 0, так что всюду между катодом и анодом на электроны действует только ускоряющее поле. Результирующая кривая eV(x)максимума не имеет. Схематически вид зависимостей
наибольшая у катода, то во всем межэлектродном пространстве E(х) < 0, так что всюду между катодом и анодом на электроны действует только ускоряющее поле. Результирующая кривая eV(x)максимума не имеет. Схематически вид зависимостей 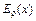 ,
, 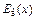 и E(х),а также eVr(x), eVв(x)и eV(x)показан на рис. 11.1, а и б. Очевидно, что при E(0) < 0 через диод протекает ток j, равный току насыщения катода js. Будем называть этот режим режимом тока насыщения.
и E(х),а также eVr(x), eVв(x)и eV(x)показан на рис. 11.1, а и б. Очевидно, что при E(0) < 0 через диод протекает ток j, равный току насыщения катода js. Будем называть этот режим режимом тока насыщения.
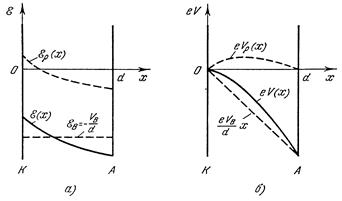
Рис. 11.1
2) E(0) > 0 . Это означает, что Er(0) > 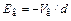 . Так как по мере удаления от катода Er(х)уменьшается и проходит через нуль, кривая E(х)также будет проходить через нуль, а зависимость eV(х) иметь максимум eVm (рис. 11.2, а и б). В этом случае анода достигнут только те электроны, энергии Wx0которых достаточны для того, чтобы преодолеть потенциальный барьер; через диод протекает ток j, меньший js. Такой режим; работы (j < js) будем называть режимом ограничения тока объемным зарядом.
. Так как по мере удаления от катода Er(х)уменьшается и проходит через нуль, кривая E(х)также будет проходить через нуль, а зависимость eV(х) иметь максимум eVm (рис. 11.2, а и б). В этом случае анода достигнут только те электроны, энергии Wx0которых достаточны для того, чтобы преодолеть потенциальный барьер; через диод протекает ток j, меньший js. Такой режим; работы (j < js) будем называть режимом ограничения тока объемным зарядом.
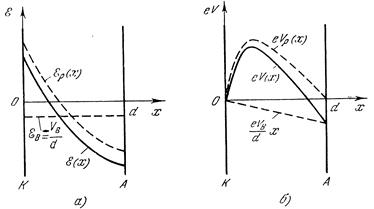
Рис. 11.2
3) E(0) = 0. Это означает, что Er (0) = 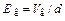 . Тогда при всех х > 0 напряженность поля E (x) < 0. Кривая eV(х) имеет максимум лишь при х = 0 (рис. 11.3, а и б). При этом j = js. Очевидно, что режим тока насыщения в данном диоде наблюдается при больших Vв, чем режим ограничения тока объемным зарядом. В последнем режиме очевидно, что чем ниже Vв, тем меньше j по сравнению с js. Случай E(0) = 0, соответствующий некоторому значению Vв = Vв*,разделяет указанные две области Vв. Хотя при этом j = js, чтобы отличить этот режим от режима, при котором (0) < 0, будем его называть переходным.
. Тогда при всех х > 0 напряженность поля E (x) < 0. Кривая eV(х) имеет максимум лишь при х = 0 (рис. 11.3, а и б). При этом j = js. Очевидно, что режим тока насыщения в данном диоде наблюдается при больших Vв, чем режим ограничения тока объемным зарядом. В последнем режиме очевидно, что чем ниже Vв, тем меньше j по сравнению с js. Случай E(0) = 0, соответствующий некоторому значению Vв = Vв*,разделяет указанные две области Vв. Хотя при этом j = js, чтобы отличить этот режим от режима, при котором (0) < 0, будем его называть переходным.
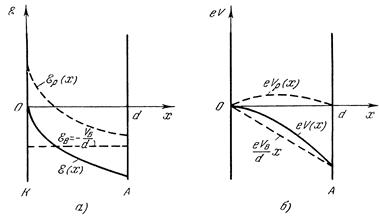
Рис. 11.3
Из приведенных качественных рассуждений вытекает, что вольт-амперная характеристика диода j(Vв) имеет вид, схематически показанный на рис. 11.4.
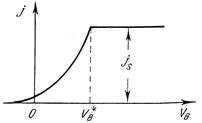
Рис. 11.4
11.2 Общая схема расчета самосогласованных полей
и объемных зарядов
Выпишем сначала необходимые соотношения в общем виде. Пусть катод и анод имеют произвольную форму. Начало отсчетавыберем в некоторой произвольной точке О. Тогда основными уравнениями будут следующие:
1. Уравнение Пуассона, связывающее потенциал электрического поля с плотностью объемных зарядов:
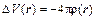 . (11.7)
. (11.7)
2. Уравнение, связывающее элементарную плотность тока dj,создаваемую в некоторой точке пространства группой электронов, имеющей в этой точке скорость vi,со скоростью vi и плотностью объемного заряда dri,создаваемого этой группой электронов:
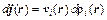 . (11.8)
. (11.8)
Очевидно, что
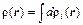 (11.9)
(11.9)
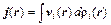 , (11.10)
, (11.10)
где интегрирование надо провести по всем группам электронов, проходящих через точку r.
3. Закон сохранения энергии
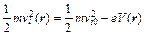 , (11.11)
, (11.11)
где vi0 начальная скорость электрона.
В общем виде выражение для электрического поля в диоде не найдено. Задача решена для некоторых частных, наиболее простых и в то же время представляющих наибольший практический интерес, случаев. Во-первых, задача решена для электронов нулевых начальных энергий в случаях плоской, цилиндрической и сферической конфигураций электродов и, во-вторых, для электронов с максвелловским распределением скоростей в случае плоских электродов.
Прежде всего рассмотрим те упрощения уравнений (11.7) (11.11), которые следуют из пренебрежения начальными энергиями электронов. Из предположения vi0=0 вытекает равенство энергий всех электронов, движущихся в точке r и одинаковость направлений их движения. Вынося одинаковое для всех электронов значение скоростей vi (r) из-под интеграла в (11.10) и отбрасывая 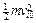 в (11.11), получим
в (11.11), получим
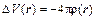 , (11.12)
, (11.12)
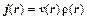 , (11.13)
, (11.13)
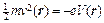 . (11.14)
. (11.14)
При этом векторное равенство (11.13) можно привести к скалярному:
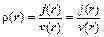 , (11.15)
, (11.15)
в котором для того, чтобы получить правильный знак 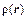 , необходимо иметь в виду, что для электронов (или отрицательных ионов) j и v имеют разные знаки, тогда как для положительных ионов одинаковые знаки.
, необходимо иметь в виду, что для электронов (или отрицательных ионов) j и v имеют разные знаки, тогда как для положительных ионов одинаковые знаки.
Учитывая (11.15) и (11.14), получим
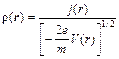 . (11.16)
. (11.16)
Тогда, подставляя в (11.12) значение 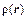 , согласно (11.16), имеем
, согласно (11.16), имеем
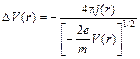 . (11.17)
. (11.17)
Для удобства решения перейдем в уравнении (11.17) к абсолютным значениям входящих в него величин, которые обозначим так:
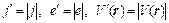 .
.
Тогда в случае е < 0 имеем
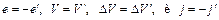 ,
,
и уравнение (11.17) перепишется в виде
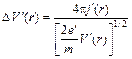 . (11.18)
. (11.18)
Аналогичным образом для е > 0 получим
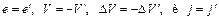
и уравнение (11.17) также принимает вид (11.18).
Таким образом, для случая нулевых начальных энергий система уравнений (11.12)(11.14) приводит к уравнению (11.18).
Дата добавления: 2015-08-11; просмотров: 1561;
