Плоскопараллельная электродная система

Рассмотрим теперь упрощения задачи, вытекающие из плоской конфигурации электродов. Для плоского случая все величины могут зависеть только от одной переменной х. Кроме того, для плоского диода в стационарном состоянии имеем

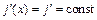. (11.19)

При указанных условиях уравнение (9.18) принимает вид

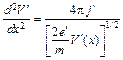(11.20)

или

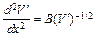, (11.21)

где

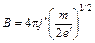
Помножив уравнение (11.21) на 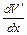, получим

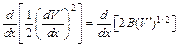
откуда первый интеграл уравнения (11.21) равен

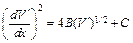, (9.22)

где С  постоянная интегрирования. Определим величину С для случая

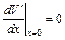. (11.23)

Условие (11.23) при нулевых начальных энергиях электронов соответствует значениям 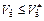. Из (11.22) и (11.23) получаем С = 0. Тогда

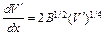. (11.24)

Интегрируя уравнение (11.24), получим

,

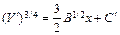где С'  постоянная интегрирования, которая определяется из условия V' = 0 при x = 0; отсюда С' = 0. Тогда

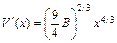.(11.25)

Подставляя в (11.25) значение B, получим

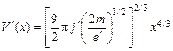(11.26)

и, следовательно,

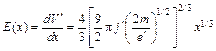(11.27)

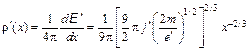(11.28)

Распределения потенциала, напряженности поля и плотности объемных зарядов, определяемых уравнениями (11.26)(11.28), изображены на рис. 11.5.

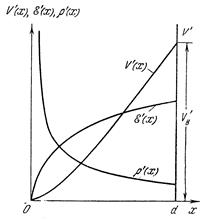
Рис. 11.5

Подставляя в (11.26) х = d,найдем V_в, необходимую для того, чтобы диод мог пропустить ток j'. С другой стороны, разрешив (11.26) относительно j' и подставив в него также х = d,можно найти ток j', который может протекать через диод при разности потенциалов V'_в:

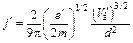. (11.29)

Таким образом, формула (11.29) определяет «токовую пропускную способность» плоского диода при данном V'_в. В случае, если определенный по (11.29) ток j' < j'_s, диод при выбранном значении j' работает в режиме ограничения тока объемным зарядом. При j' = j_s 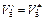. Таким образом, формула (11.29) является вольт-амперной характеристикой плоского диода при 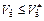в приближении нулевых начальных энергий электронов. Подставляя численные значения входящих в (11.29) величин, выражая j' в а×см^2, V' в вольтах и d  в см, получим

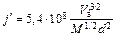, (11.30)

где М  молекулярный вес вещества заряженных частиц, который для электронов равен 1/1840. Тогда для электронов имеем

.

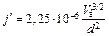Проанализируем теперь применимость полученных формул к реальным эмиттерам, у которых v₀ ¹ 0. Прежде всего заметим, что формулы выведены для случая 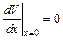. Для реального эмиттера это условие выполняется только для переходного режима, т. е. при 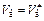. Далее, из формулы (11.28) следует, что r(0) = ¥. Этот результат вытекает уже из формулы (11.13) при v(0) = 0. 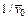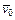В реальном диоде из-за наличия начальных скоростей у термоэлектронов приближенно имеем r(0) = , где  средняя начальная скорость термоэлектронов. Так как V(х)и E(х)определяются r(x), то и значения потенциала и напряженности поля вблизи катода, описываемые формулами (11.26) и (11.27), также отличны от реальных. Поскольку в действительности r(x)у катода меньше ее теоретического значения, определяемого (11.28), то и значения V(х)и E(х)у катода в реальном эмиттере меньше значений, даваемых (11.26) и (11.27). Область указанных заметных отклонений простирается от катода на расстояния, где начальные энергии электронов сравнимы с энергиями, полученными в межэлектродном промежутке, т. е. eV'(x)» 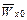= kT. Так как 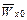составляют сотые или десятые доли эв,то при 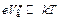,что во многих случаях имеет место, рассматриваемая область вблизи катода мала, так что для реальных диодов в большей части межэлектродного пространства найденные по (11.26)(11.28) значения r'(x), E'(х)и V'(х)мало отличаются от действительных. Что касается величины 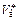при фиксированном значении тока j_s, то в силу сказанного выше она окажется несколько меньше, чем это следует по (11.29). Однако при 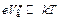это различие незначительно.

Таким образом, формула (11.29) достаточно хорошо определяет «токовуюпропускную способность» реального плоского диода для режима 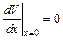, если .

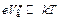Обсудим теперь вопрос о возможности применения полученных формул для реального плоского диода при работе его в режиме ограничения тока объемным зарядом, т. е., когда 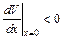(рис. 11.5). Обратим внимание на то, что в этом случае в плоскости х = х_т выполняется условие 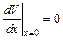. Следовательно, для области пространства от х_т до d при условии, что 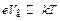,можно использовать полученные выше формулы. Тогда «токовая пропускная способность» этой части диода приближенно определяется уравнением (11.29), в котором, очевидно, следует заменить 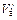величиной 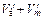,a d  величиной d  x_m,т. е.

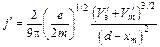(11.31)

При 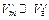и x_m = d формула (11.31) совпадает с (11.29). Указанные неравенства при 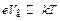,как будет показано в следующем параграфе, обычно выполняются.

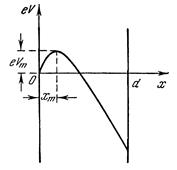
Рис. 11.5

Таким образом, формула (11.31) (или менее точная формула (11.29)) приближенно является вольт-амперной характеристикой реального плоского диода при 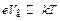. Это означает, что при работе реального плоского диода в режиме ограничения тока объемным зарядом при данном 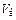в межэлектродном пространстве возникает потенциальный барьер, который обеспечивает прохождение через него такой доли тока эмиссии катода j_s, которая примерно находится в соответствии с законом (11.29). При eV_в ,лишь несколько превосходящих kТ или сравнимых с kТ,вольт-амперная характеристика описывается формулами, отличными от полученных выше.

Отметим, что при учете начальных скоростей становится ясным механизм, который делит эмитируемый катодом поток электронов на два: поток, проходящий через диод, и поток, который возвращается на катод. Именно величина начальной скорости электрона определяет, пройдет ли электрон над потенциальным барьером.