Джоулев механизм вакуумного пробоя

Итак, существуют два критерия вакуумного пробоя (12.1) и (12.3). Первый относится к импульсному пробою, а второй к стационарному. Основная задача теории вакуумного пробоя состоит в том, чтобы дать теоретическое объяснение этим критериям. Обычно критерии вакуумного пробоя выводят из условия достижения некоторой критической температуры (например, плавления) на поверхности катода или анода. По нашему мнению, критерии (12.1) и (12.3) отражают условия достижения критической удельной энергии в микрообъеме катода w_с, необходимой для его взрыва, которая обычно в несколько раз превосходит удельную энергию сублимации w_с. Откуда берется эта энергия? Это энергия джоулева разогрева микроучастков катода. Посмотрим, как эта энергия выделяется.

В простейшем случае форму микроострий на катоде можно считать цилиндрическими. Действительно, если средняя напряженность электрического поля составляет 10⁶В/см, а для микровзрыва за время ~10^-8с необходимо иметь поле 10⁸В/см, то усиление электрического поля должно быть b_Е ~ 10². Это означает, что высота острия в десятки и сотни раз превосходит радиус его кривизны, то есть острия можно считать цилиндрическими. В этом случае можно принять, что теплоемкость металла меняется мало, поэтому вместо удельной энергии w_К можно использовать температуру острия в уравнении, описывающем его нагрев.

Нагрев цилиндрического острия описывается уравнением

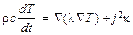, (12.4)

где r, c, l, k- соответственно плотность материала эмиттера, удельная теплоемкость, теплопроводность и удельное электрическое сопротивление. В правой части уравнения (12.4) первый член описывает перенос тепла из-за теплопроводности, а второй - выделение тепла за счет джоулева нагрева. Значения параметров r, с, l, k в общем виде зависят от температуры, но в наибольшей степени от нее зависит удельное сопротивление. Представим его в форме

k=k₀T. (12.5)

Такой вид зависимости k(T) с погрешностью не более 20% описывает экспериментальные результаты для многих электродных материалов в диапазоне температур примерно от 300° К до температуры плавления. Плавление приводит к значительному увеличению k. Отметим, что удельная теплота плавления превосходит удельную теплоемкость, для меди в 400 раз, а для вольфрама - в 1300. Для испарения требуется значительно больше тепла. Теплота испарения в 20-30 раз больше удельной теплоты плавления. Для меди и алюминия она равна 3 эВ в расчете на один атом.

Для стационарного случая или длительных импульсов напряжения, когда можно принять dT/dt = 0, и катодного выступа в виде цилиндра высотой h уравнение (12.4) с учетом (12.5) дает следующее распределение температуры T(x) по высоте выступа:

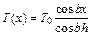, (12.6)

где T₀ - температура основания выступа; x - расстояние, измеренное от вершины выступа; b = j(k₀/l)^1/2.

Из (12.6) следует, что температура кончика выступа (x = 0) стремится к бесконечности при bh = p/2. Следовательно, предельное значение плотности тока можно найти из формулы

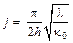. (12.7)

Например, для выступа с высотой h = 1 мкм для меди, вольфрама и никеля j = = 3×10⁸; 1.0×10⁸и 0.5×10⁸А/см², соответственно.

При коротких длительностях импульсов предельная плотность тока АЭЭ превышает таковую в стационарном случае. Если длительность импульса много меньше, чем время перехода острия в стационарное нагретое состояние, то имеет место соотношение

t_и † 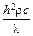(12.8)

Например, если для вольфрама h = 0.6 мкм, то соотношение (12.8) выполняется уже при t_и = 10 нс. Если соблюдается условие (12.8), а начальная плотность тока j неизменна во времени, то из уравнения (12.3) с учетом (12.4) следует, что температура растет экспоненциально со временем по закону

T = T₀ exp j²k₀t/rc. 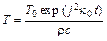(12.9)

Если условно принять, что взрыв острия наступает при достижении некоторой критической температуры T_к, то время задержки взрыва определится из соотношения

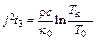. (12.10)

Следовательно, формулы (12.7) и (12.10) дают результат, качественно согласующийся с экспериментом. Т.к. эти критерии были получены с учетом джоулева разогрева микроострий, то эту модель вакуумного пробоя называют джоулевой.

Стационарная задача о разогреве острийного катода автоэмиссионным током большой плотности была ранее рассмотрена Дайком с сотрудниками. Ими было получено следующее выражение для температуры вершины эмиттера:

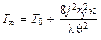, (12.11)

где q - полуугол раствора конуса.

Для типичных размеров автоэмиттера из вольфрама плотность тока, необходимая для нагрева вершины до Т_пл, составляет 10⁷А/см². Формула (12.11) тоже приводит к критерию, аналогичному (12.3). Впоследствии Вибранс улучшил эти расчеты введением зависимости удельного сопротивления и плотности тока от температуры и распространения их на случай малых микроострий на плоских электродах. В этом случае следовало, что из-за роста удельного сопротивления с температурой эмиттер становится неустойчивым в тепловом отношении при температурах, существенно меньших Т_пл. В дальнейшем в ряде работ было учтено также влияние эффекта Ноттингама на тепловой баланс микроострия. Необходимо отметить, что хотя влияние эффекта Ноттингама на нагрев острия и значительно, но на характер критериев (12.1) и (12.3) он не влияет, а изменяет только величины констант.

Итак, мы показали, что при преимущественном влиянии на пробой катодных микроострий существует два критерия пробоя, которые записываются соотношениями (12.1) и (12.3). Первый относится к импульсному пробою, а второй – к статическому. Физическая сущность этих критериев одинакова. За счет высокой плотности тока АЭЭ происходит джоулев разогрев микроострий и их взрыв. Оба критерия обозначают, что микрообъем металла получает удельную энергию, которая существенно превосходит энергию сублимации. Однако достижение определенной удельной энергии микровзрыва является условием необходимым, но недостаточным для перехода пробоя в искру. Для этого еще необходима определенная масса вещества, участвующая во взрыве. Учитывая, что удельная энергия взрыва благодаря критериям (12.1) и (12.3) считается заданной, необходимость определенной массы вещества эквивалентна достижению необходимой абсолютной величины энергии в микровзрыве. Только при соблюдении этих двух критериев разряд переходит в искровую стадию и становится самоподдерживающимся.

12.6 Вольт-амперная характеристика искрового разряда

Рассмотрим вакуумный диод с острийным иди плоским катодом на котором функционирует одиночный КФ. Соотношений, описывающих вольт-амперную характеристику таких диодов, не известно. Будем полагать что плазма КФ находится под потенциалом катода, имеет сферическую эмиттирующую поверхность с неограниченной эмиссионной способностью. Качественно ясно, что при ограниченной эмиссионной поверхности катода объемный заряд электронов будет слабее возмущать потенциал любой точки межэлектродного пространства, чем при неограниченной. Это должно привести к увеличению предельной плотности тока в вакуумном промежутке. Будем использовать приближенный расчет плотности тока в диоде с бесконечными плоскопараллельными электродами для случая, когда неограниченной эмиссионной способностью обладает небольшой участок катода радиусом r,а радиальное расталкивание пучка объемным зарядом отсутствует. Чем меньше отношение r/d,тем больше k₀= j_r/j_¥ ( j_r  истинная плотность тока, j_¥ плотность тока из закона Ленгмюра для бесконечных плоских электродов).

Воспользовавшись таким подходом и представляя площадь эмиссии электронов в виде 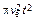,а расстояние между фронтом плазмы и анодом через ,можно записать:

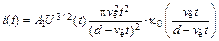(12.12)

где А₁= 2,33×10^6А/В^3/2. Из (12.12) следует, что первеанс электронного потока Р = = i(t)/ 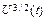должен быть однозначной функцией отношения 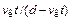. Для проверки справедливости этого вывода было обработано большое количество осциллограмм тока в устойчивой стадии эмиссии, полученных с хорошим амплитудным и временным разрешением в диапазоне экспериментальных условий: d =14 мм, U₀= 2040 кВ и d = 610 мм, U₀= 80120 кВ; катод  игла. Некоторые из экспериментальных точек, произвольно выбранные из большого количества (~300), приведены на рис. 12.3, а (кривая 1). Здесь принята скорость v_к= 2×10⁶см/с. Можно видеть, что большинство точек ложится на одну плавную кривую. Это же в полной мере относится и ко всем другим обработанным данным, не нанесенным на график для значений 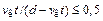. На этом же рисунке дана зависимость P( 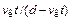)для k₀= 1 (кривая 2). Нетрудно видеть, что применение закона «степени 3/2», не учитывающего ограниченности эмиссионной поверхности, дает заниженные на один-два порядка значения электронного тока.

Для системы с плоскими электродами и одиночным КФ, возникшим на месте искусственно созданного микровыступа (U₀ = 2040 кВ, d = 0,31,0 мм), экспериментальные точки лучше всего укладывались на одну кривую Р = f(v_кt/d)(рис. 12.3, б).

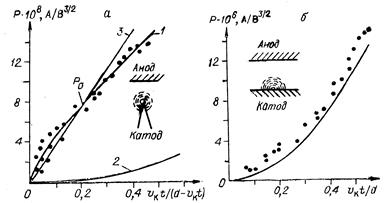
Рис. 12.3.Зависимости первеанса электронного потока от отношения v_кt/(d  v_кt)для случая факела на острийном катоде (а) и от отношения v_кt/d для случая факела на плоском катоде (б). а  1  эксперимент; 2  расчет для плоского случая; 3  расчет по (12.3);. б  точки  эксперимент; сплошная линия  расчет.

Выражение, подобное (12.12), было получено аналитически. Плотность тока в каждой точке эмиттирующей сферической поверхности определялась, пользуясь известной формулой БогуславскогоЛенгмюра (11.29). Длина эффективного промежутка (эффективную длину траектории электрона выходящего из данной точки эмиттирующей поверхности) можно определялась из выражения d_эфф = U/E,где Е  напряженность электрического поля в данной точке сферы в отсутствие объемного заряда электронов. Следовательно, задача сводится к нахождению напряженности электростатического поля на катоде в произвольной системе электродов. Затем полный ток в промежутке определяется путем интегрирования плотности тока по эмиттирующей поверхности. Для случая, когда КФ функционирует на вершине острия получено:

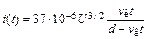. (12.3)

Зависимость (12.3) представлена на рис. 12.3, а (линия 3).Она удовлетворительно согласуется с экспериментальными результатами. При этом k₀» 5 .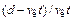

Для случая полусферической эмиттирующей поверхности на плоском катоде аналогичным образом получено:

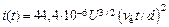. (12.4)

Эта зависимость показана на рис. 12.3 б и также хорошо согласуется с экспериментальными данными при k₀ » 6.

Заметим, что поскольку напряженность электрического поля в эффективном диоде находилась из выражений, справедливых при условии v_кt = d,то и соотношения (12.3) и (12.4) можно использовать только при выполнении этого условия.

Литература

1. Л.Н. Добрецов, М.Б. Гомоюнова. Эмиссионная электроника. «Наука», Москва, 1966.

2. М.И. Елинсон, Г.Ф. Васильев. Автоэлектронная эмиссия. «ГИФ-МЛ», Москва, 1958.

3. В.Л. Грановский. Электрический ток в газе. Том 1. «ГИТ-ТЛ», МоскваЛенинград, 1952.

4. К. Шимони. Физическая электроника. «Энергия», Москва, 1977.

5. Г. Мирдель. Электрофизика. «Мир», Москва, 1972.

6. В.Д. Соболев. Физические основы электронной техники. «Высшая школа», Москва, 1979.

7. Ненакаливаемые катоды. Под редакцией М.И. Елинсона. «Наука», Москва, 1974.

8. Р. Фишер, Х. Нойман. Автоэлектронная эмиссия полупроводников. «Мир», Москва, 1971.

9. А. Модинос. Авто- термо- и вторично- электронная эмиссионная спектроскопия. «Наука», Москва, 1990.

10. В.И. Фистуль. Физика и химия твердого тела. Том 1, Том 2. «Металлургия», Москва, 1995.

11. Г.А. Месяц, Д.И. Проскуровский. Импульсный электрический разряд в вакууме. «Наука», Новосибирск, 1984.

12. Г.А. Месяц. Эктоны, Часть 1, 2, 3. УИФ «Наука», Екатеринбург, 1993-1994.

13. Г.А. Месяц. Эктоны в вакуумном разряде: пробой, искра, дуга. «Наука», Москва, 2000.

14. Е. Линч, А. Николайдес. Задачи по физической электронике. «Мир», Москва, 1975.

15. Б.Н. Швилкин. Газовая электроника и физика плазмы в задачах. «Наука», Москва, 1978.

16. Б.Н. Швилкин, Н.А. Мискинова. Физическая электроника в задачах. «Наука», Москва, 1987.

17. Методические лекционные разработки