Анализ кривошипно-шатунного механизма
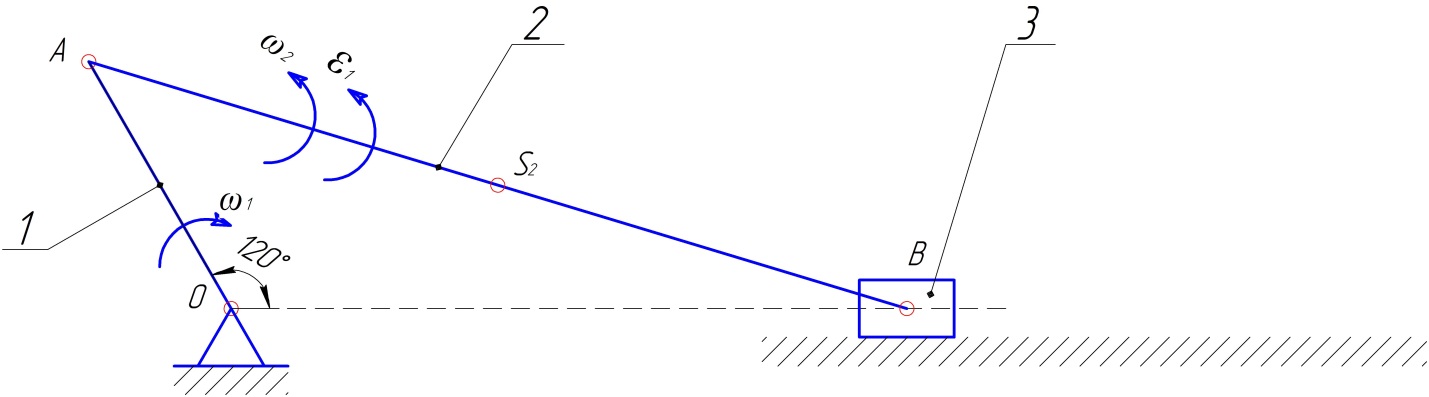
1.1. Кинематический анализ
1.1.1. Масштаб длин частей механизма
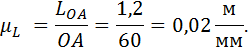
1.1.2. Длины частей механизма
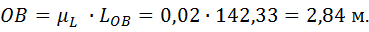
1.1.3. Определение скоростей
Проанализируем схему кривошипно-ползунного механизма: точка О является неподвижной точкой, следовательно, модуль скорости этой точки равен нулю

Вектор скорости точки А представляет собой геометрическую сумму вектора скорости точки О и скорости относительного вращательного движения точки А вокруг точки О:

Линия действия вектора скорости 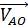 является перпендикуляром к оси кривошипа 1, а направление действия этого вектора совпадает с направлением вращения кривошипа.
является перпендикуляром к оси кривошипа 1, а направление действия этого вектора совпадает с направлением вращения кривошипа.
Модуль скорости точки А:
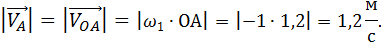
1.1.4. Масштаб скоростей
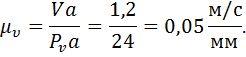
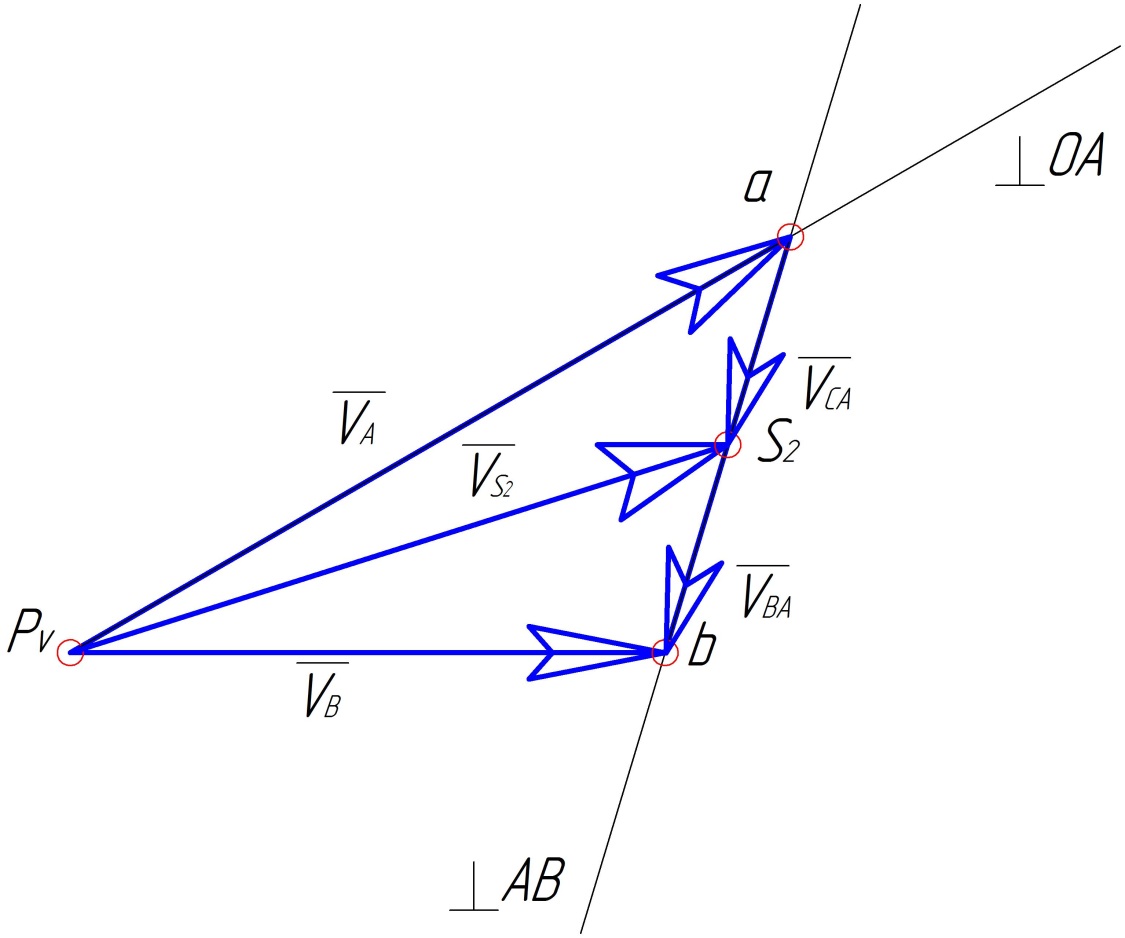
1.1.5. Треугольник скоростей
1.1.6. Величина линейных скоростей и угловые скорости
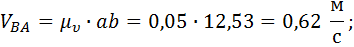
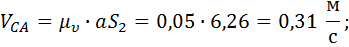
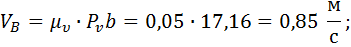
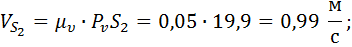
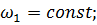
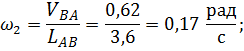
Направление вектора угловой скорости шатуна определяется следующим образом. Вектор скорости 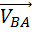 условно переносится в точку В плана механизма. Куда он будет вращать шатун относительно точки А, в ту сторону и направлена угловая скорость
условно переносится в точку В плана механизма. Куда он будет вращать шатун относительно точки А, в ту сторону и направлена угловая скорость 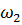 .
.
1.1.7. Определение ускорений
(۰) а полюс
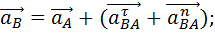
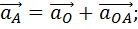
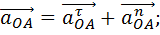
Так как точка O неподвижна и ускорение её равно нулю 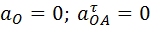
при 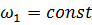 , то:
, то:
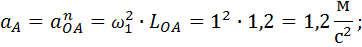
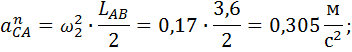
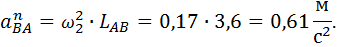
1.1.8. Масштаб ускорений
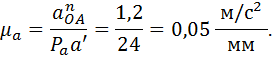
1.1.9. Определение оставшихся ускорений
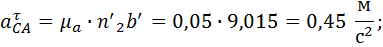
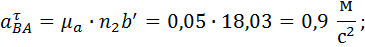
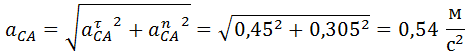
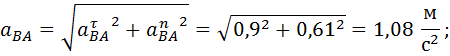
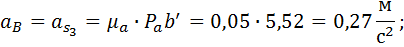
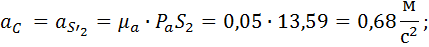
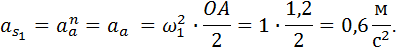
1.1.10. Треугольник ускорений
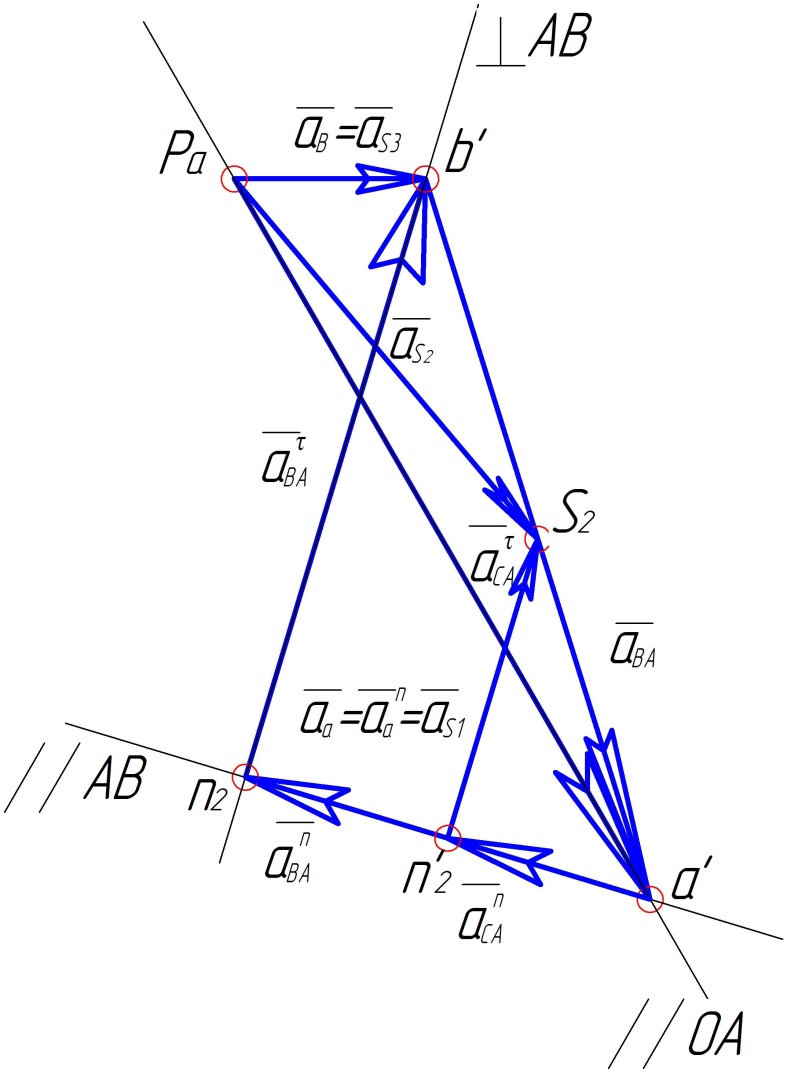
1.2. Силовой анализ
1.2.1. Сила тяжести звена
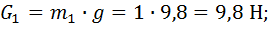
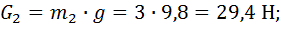
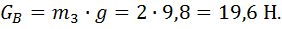
1.2.2. Сила инерции звена
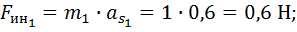
s w:val="32"/></w:rPr><m:t>Рќ;</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="006D52B3"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 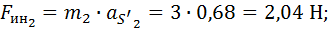
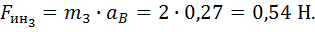
1.2.3. Осевой момент инерции звена
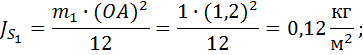
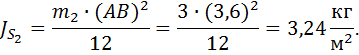
1.2.4. Угловое ускорение звена
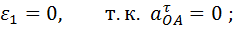
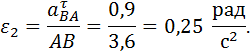
1.2.5. Момент пар сил инерции
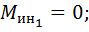
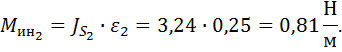
1.2.6. Силовая схема 1
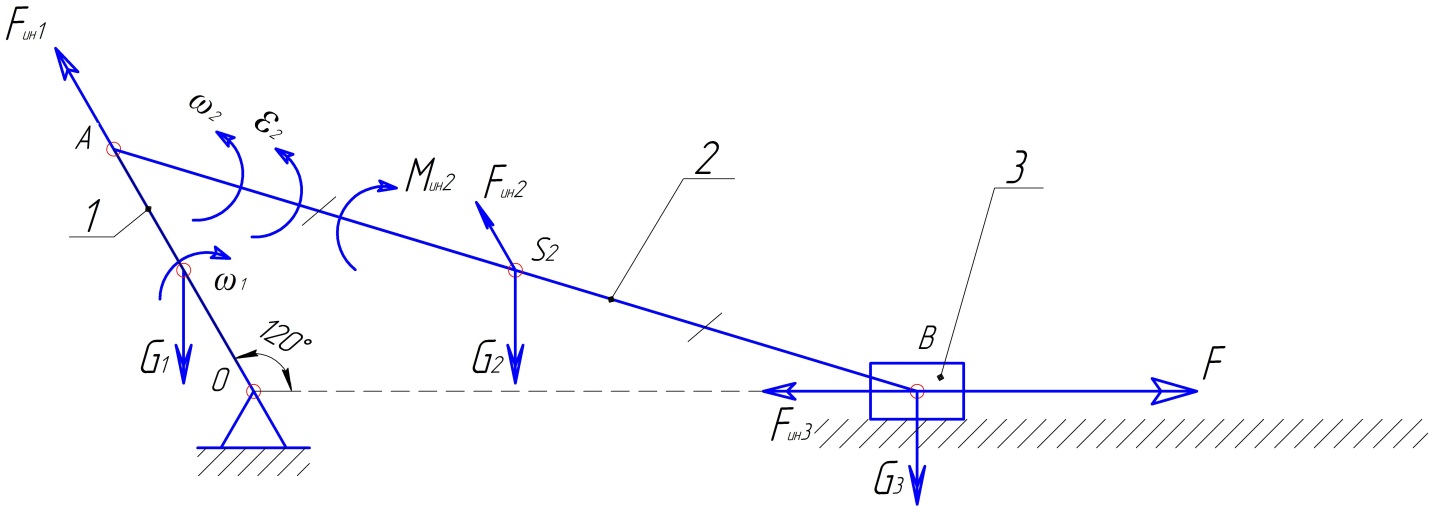
Для удобства дальнейшего расчёта силу и момент сил инерции заменим одной силой, которая будет смещена относительно центра масс звена:
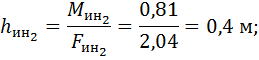
т.к. ползун перемещается только горизонтально, и G3 будет компенсироваться её реакцией, то в расчёт их брать не буду.
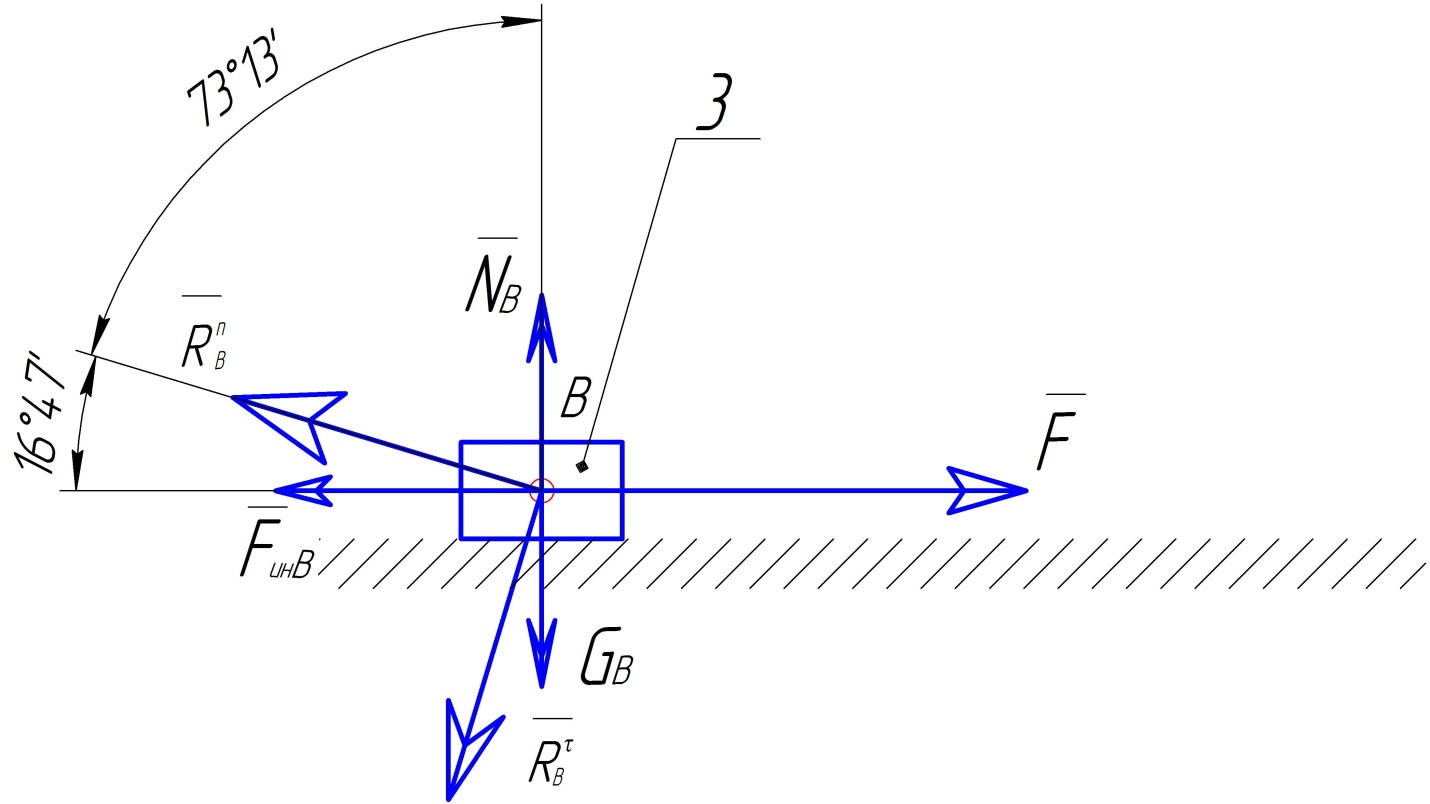
1.2.7. Силовой расчёт структурной группы
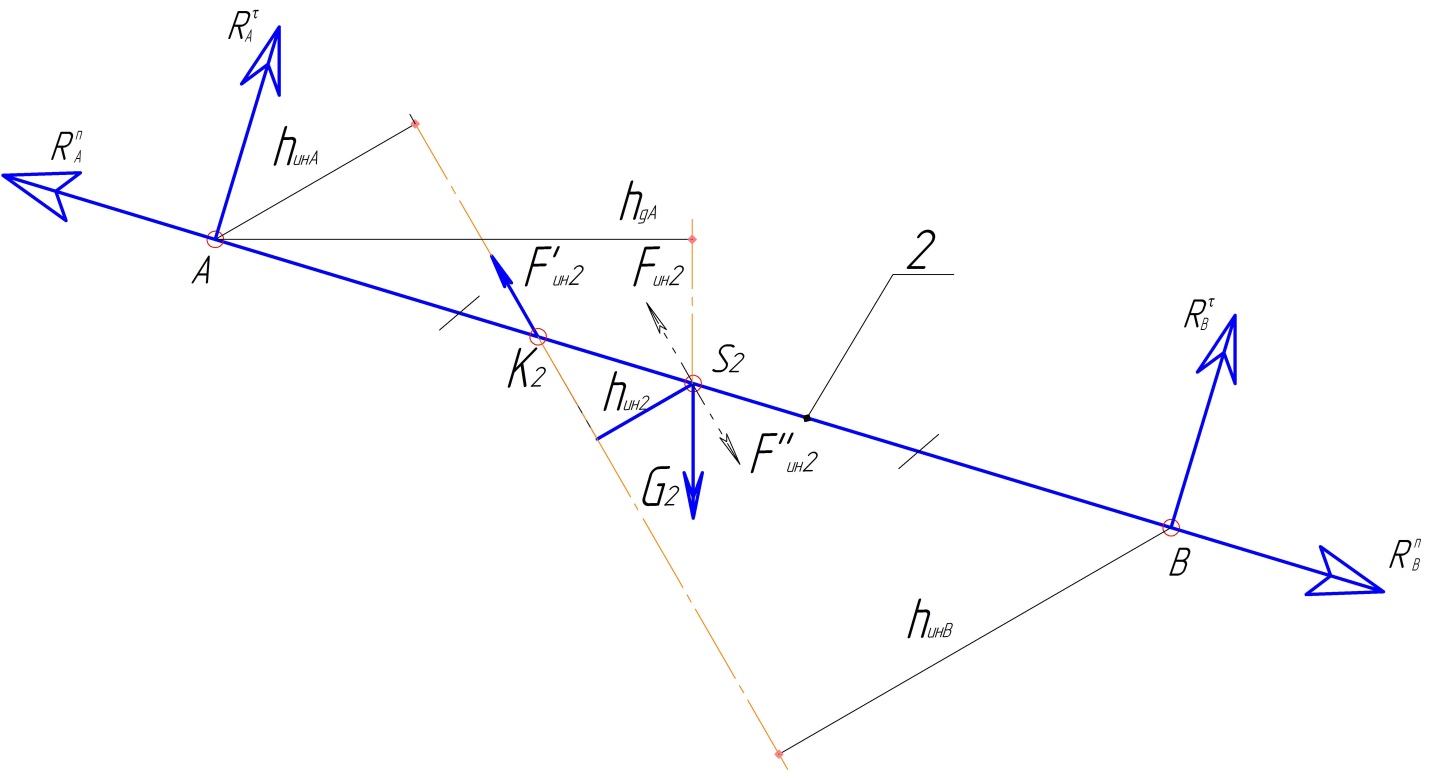
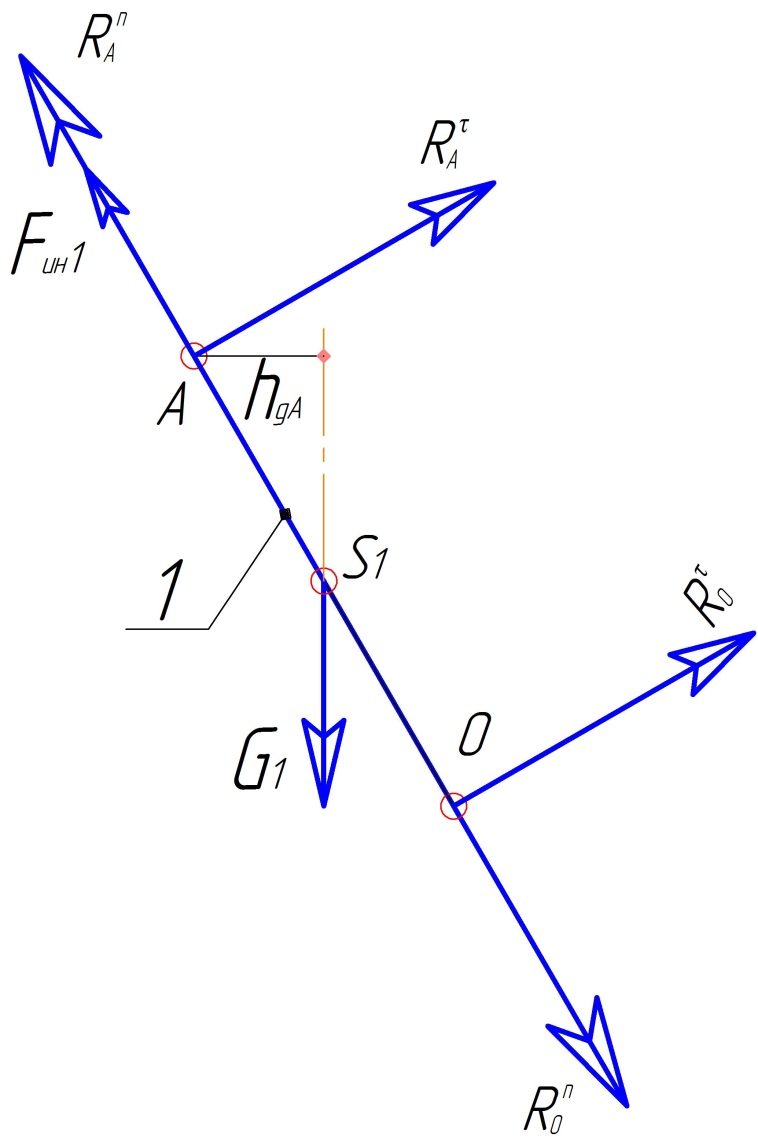
Показываю все внешние силы, силы инерции, а действие отброшенных частей звена OA и опоры B заменяю реакциями. Эти реакции во вращательной паре неизвестны, поэтому показываем их в виде геометрической суммы нормальной, направленной вдоль звена и тангенциальной, направленной перпендикулярно звену, составляющих.
Если направление реакций выбрано неверно, то в результате расчёта получим отрицательное значение.
1.2.8. Определение реакции
Звено 2
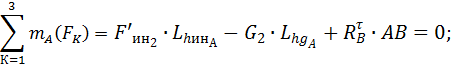
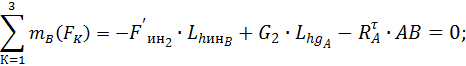
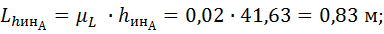
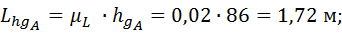
t wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr><m:t>=0,02в€™81,63=1,63 Рј;</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="000E16FC"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 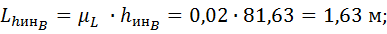

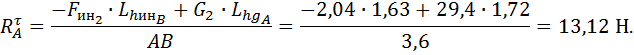
Звено 1
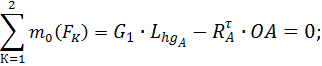
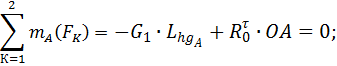
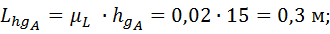
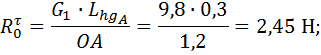
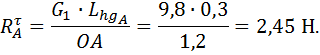
Звено 3
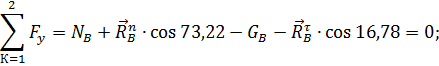
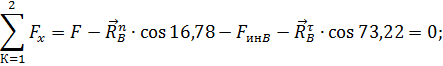
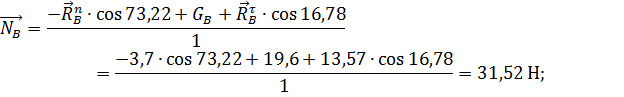

1.2.9. Уравнение равновесия сил
действующих на звено 1
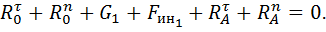
действующих на звено 2
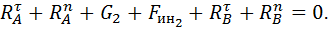
действующих на звено 3
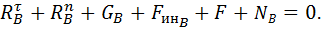
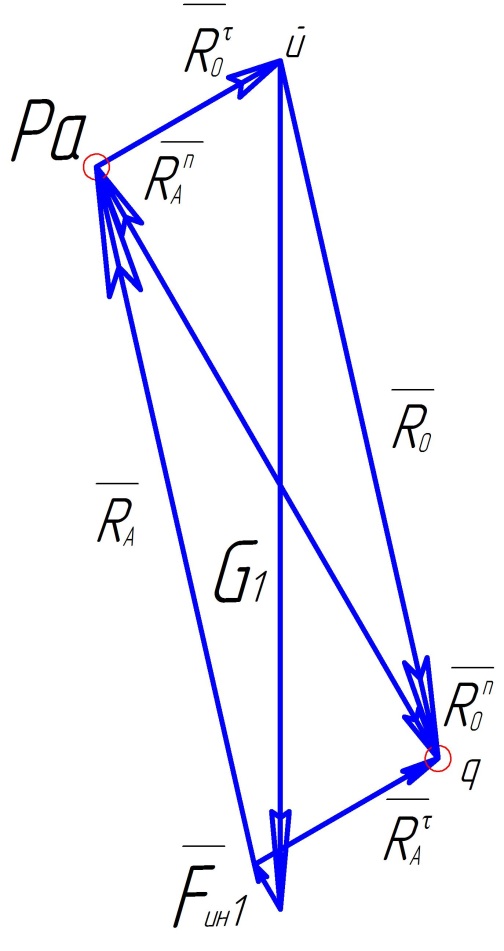
1.2.10. Построение векторов сил и определение реакций
Звено 1
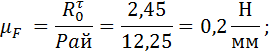
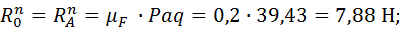
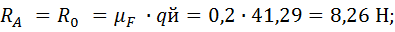
Звено 2
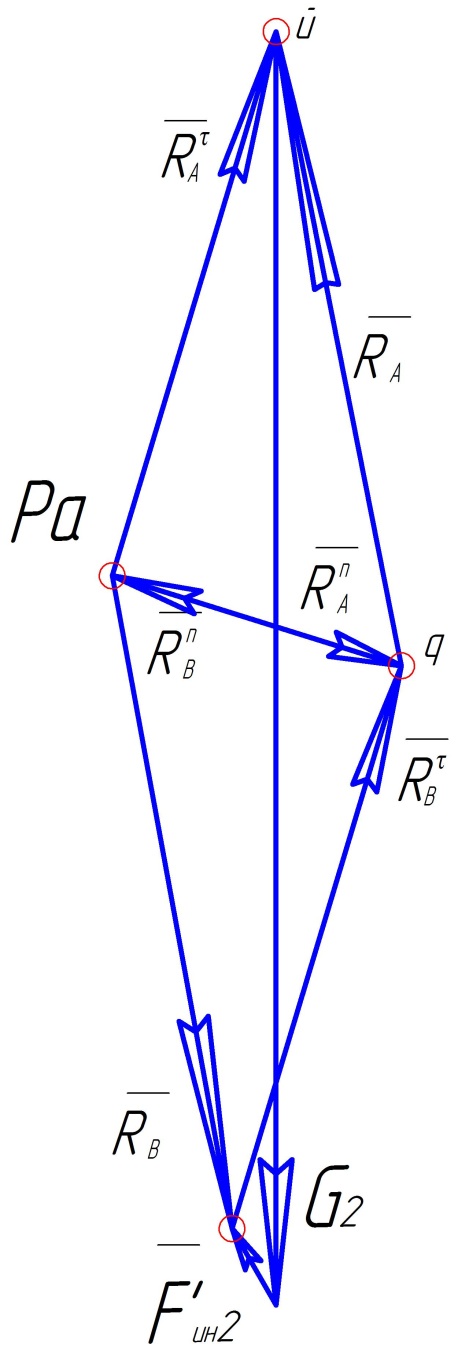
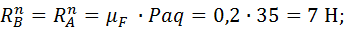
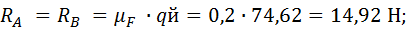
Звено 3
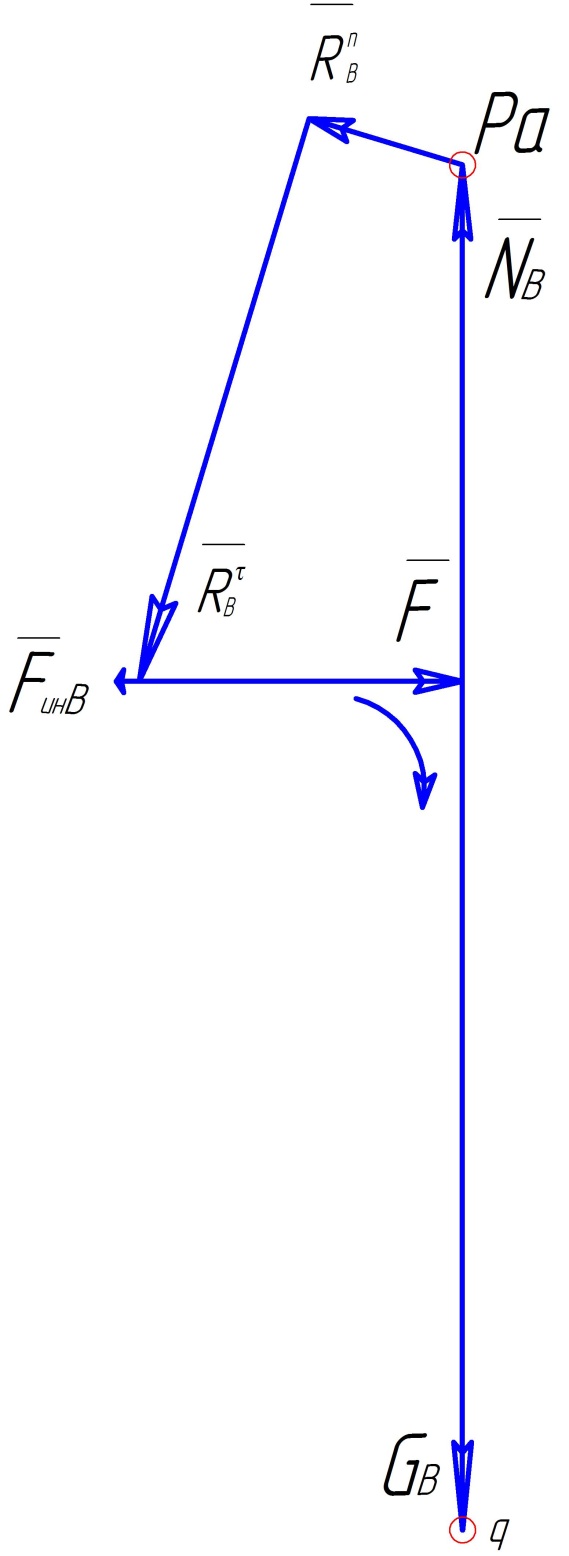
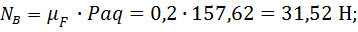
Графические и расчётные данные совпадают, значит всё выполнено верно.
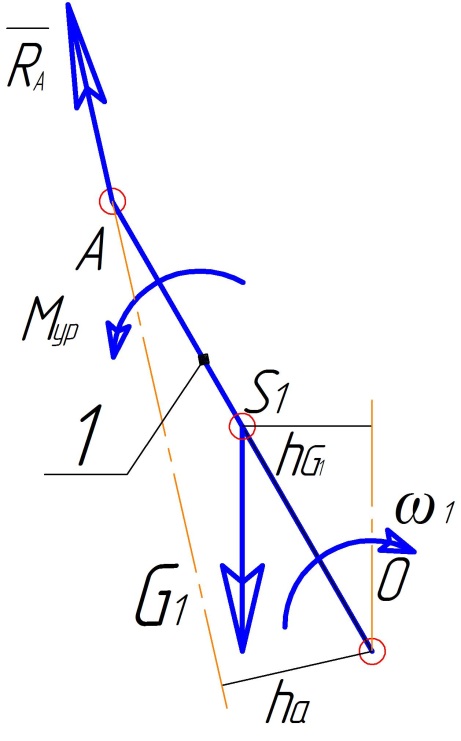
1.3. Определение уравновешивающего момента
1.3.1. Уравновешивающий момент для ведущего звена
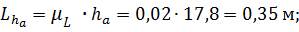
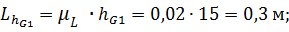
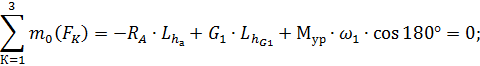
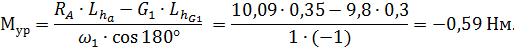
| <== предыдущая лекция | | | следующая лекция ==> |
| Дискретні системи управління | | | Теория фитнес-тренировки |
Дата добавления: 2015-07-24; просмотров: 8078;
