Вторичная электронная эмиссия

При бомбардировке металлической поверхности электронами последняя эмигрирует электроны. Это и есть вторичная электронная эмиссия. Определим коэффициенты вторичной эмиссии или к.п.д. этой эмиссии с помощью соотношения :

.

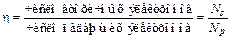Как показывают измерения, h зависит от числа первичных электронов, угла падения, материала и. физического состояния поверхности. Согласно измерениям h различных материалов изменяется как функция энергии W_p падающих электронов соответственно кривым, приведенным на рис. 4-48, а.

Как видно из графиков, h сначала повышается вместе с энергией падающих (первичных) электронов, достигает максимума (табл. 10.1) и затем начинает уменьшаться. Качественно это явление объясняется следующим образом; падающие электроны передают свою энергию электронам металла. Если сумма переданной и собственной энергии электрона металла больше, чем работа, необходимая для выхода, то электрон металла может покинуть металл.

Таблица 10.1. Вторичная эмиссия (численные значения для некоторых веществ)

Вещество		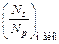Энергия первичных электронов, эВ	Вещество		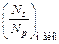Энергия первичных электронов, эВ
А1 Cu Fe Ni	0,97 1,35 1,32 1,3		W MgO BeO BaO–SrO	1,43 8,2 10,2

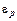Если электрон с энергией падает на твердую поверхность, он может рассеяться обратно в вакуум упруго или неупруго. На практике величина 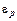лежит, как правило, в интервале 10 < 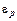< 500 эВ. Часть энергии этих электронов теряется в целом каскаде столкновений с другими, вторичными электронами. Некоторые из вторичных электронов эмиттируют из поверхности. Очевидно, что нельзя отличить первичный обратно рассеянный электрон и вторичный эмиттированный электрон. Поэтому отличие между этими двумя электронами обычно делается лишь для удобства довольно искусственным образом.

Это объяснено в подписи к рис. 10.7, на котором представлены типичные РПЭ электронов, эмиттированных из поверхности металла. Электроны в области III соответствуют упруго рассеянным электронам и электронам, которые в результате столкновений с фононами потеряли энергию порядка нескольких сотых долей электронвольта. В области II находятся электроны, потерявшие значительно большую энергию. Эта область характеризуется рядом пиков, соответствующих неупругим столкновениям первичных электронов с плазмонами и с другими электронами. Энергия этих пиков фиксирована относительно энергии первичных электронов и лежит на 2–50 эВ ниже ее. Эта величина определяется энергией возбуждения плазмонов и межзонных переходов. Область I соответствует истинно вторичным электронам, генерируемым в каскадном процессе.

Здесь мы будем рассматривать только электроны этой области, называя именно их вторичными электронами. Вследствие большого числа случайных столкновений, происходящих между начальным падением первичного электрона и конечным выходом вторичного электрона из металла, у последнего остается крайне мало информации о первичном электроне. Следовательно, форма энергетического и углового распределений вторичных электронов должна быть практически независимой от энергии 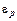и направления падения электронного пучка, если 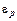достаточно велика.

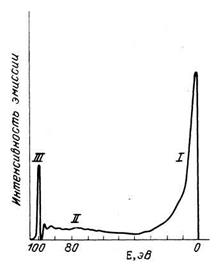
Рис. 10.7. Энергетический спектр вторичных электронов, эмиттированных из поверхности металла при его бомбардировке электронами с энергией 100 эВ ( 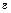– кинетическая энергия эмиттированных электронов). Электроны в области I – истинно вторичные, в области II и III – неупруго и упруго рассеянные первичные электроны

Существует множество теорий ВЭЭ из металлов, большинство из которых основано на модели металла Зоммерфельда. Эти теории (Ван дер Зил,1953; Вольфф,1954; Стрейтволъф,1959; Стольц,1959; Амелио,1970; Чанг и Эверхарт,1974; Шоу,1980) отличаются одна от другой главным образом способом аппроксимации каскадных процессов. В большинстве этих теорий для энергетического распределения вторичных электронов получены формулы, которые имеют следующий вид:

I ( 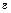)~ ( 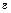+ 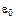)^–xР( 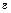), (10.4)

где 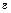– кинетическая энергия эмиттированных электронов, равная их полной энергии, отсчитываемой от уровня вакуума. Первый сомножитель в (10.4) пропорционален числу вторичных электронов с энергией 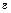, падающих на границу металл–вакуум из металла. Значения 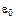и х в разных теориях различны. Так, в теории Вольффа, например, х » 2, 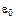= 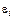,где 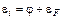– разность энергий между уровнем вакуума и дном зоны проводимости. Второй сомножитель в (10.4) – коэффициент прохождения, определяющий, какая часть электронов из металла проходит через барьер и эмиттируется в вакуум. В теории Вольффа распределение электронов по импульсам сферически симметрично, и поэтому

Р( 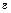) » 1 – [ 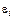/( 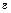+ 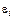)]^1/2. (10.5)

Это уравнение применимо, если анализатор энергии принимает любой электрон с энергией 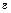независимо от направления его скорости.