Найпростіші властивості границь векторних послідовностей
Теорема 3. Якщо  має границю, то така границя одна.
має границю, то така границя одна.
Доказ. Самостійно.
Визначення 6. Послідовність  називається обмеженою, якщо існує така куля
називається обмеженою, якщо існує така куля 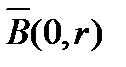 , яка містить всі елементи цієї послідовності, тобто для елементів послідовності виконується нерівність
, яка містить всі елементи цієї послідовності, тобто для елементів послідовності виконується нерівність 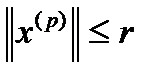 .
.
Теорема 4. Нехай  збігається, тоді
збігається, тоді  - обмежена послідовність.
- обмежена послідовність.
Зауваження. Не будь-яка обмежена послідовність є збіжною.
Теорема 5 (про покоординатну збіжність). Для того, щоб  ,
, 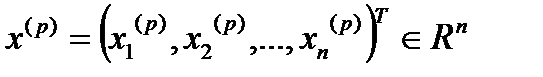 збігалася до точки
збігалася до точки 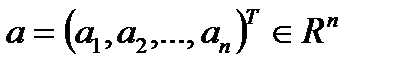 необхідно і достатньо, щоб для кожного значення
необхідно і достатньо, щоб для кожного значення 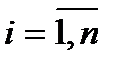 відповідна числова послідовність координат
відповідна числова послідовність координат 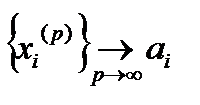 .
.
Доказ. Необхідність. Нехай 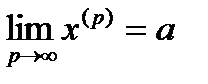 . За визначення границі векторної послідовності це означає, що
. За визначення границі векторної послідовності це означає, що
для 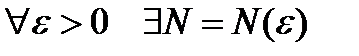 , що для
, що для 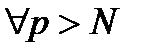 виконується:
виконується:  .
.
Візьмемо довільно конкретне значення 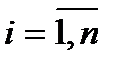 . Нехай
. Нехай 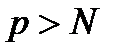 . Тоді
. Тоді
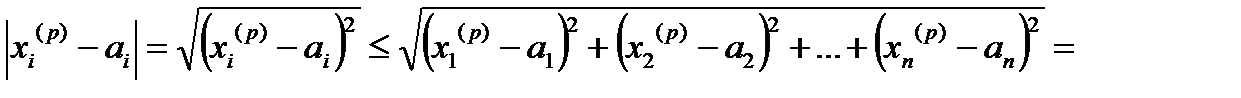
 ,
,
а це за визначенням границі числової послідовності і означає, що 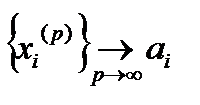 .
.
Достатність. Нехай для 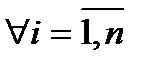 :
: 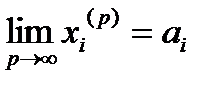 .
.
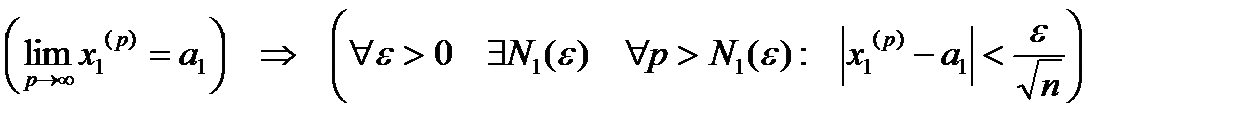 ,
,
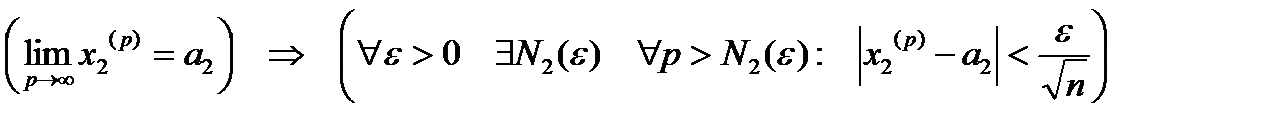 ,
,
...
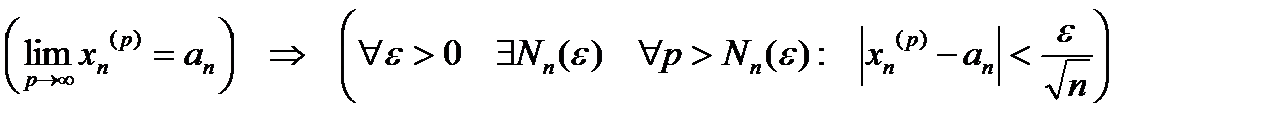 .
.
Нехай 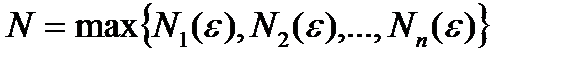 . Тоді для
. Тоді для 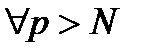 і для
і для 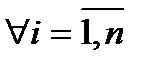 всі попередні нерівності виконуються одночасно, а тоді:
всі попередні нерівності виконуються одночасно, а тоді:
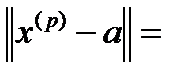
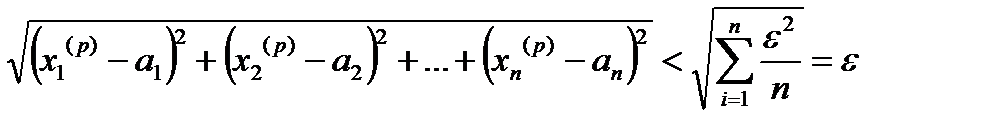 ,
,
тобто 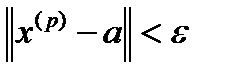 ,
,
що говоре про те, що 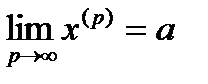 .
.
Теорема 6. Нехай  ,
, 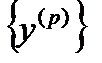 - векторні послідовності в просторі
- векторні послідовності в просторі 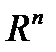 ,
, 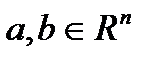 і
і 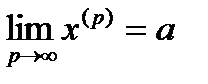 ,
, 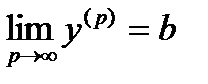 . Тоді послідовності
. Тоді послідовності 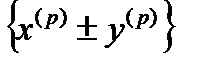 ,
, 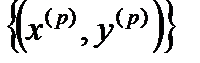 (тут
(тут 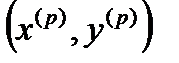 - скалярний добуток
- скалярний добуток 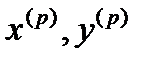 ) також є збіжними і
) також є збіжними і
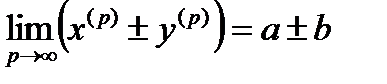 ,
, 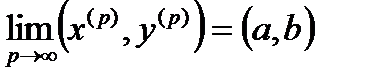 .
.
Дата добавления: 2015-08-11; просмотров: 793;
