Равносильные преобразования формул.
Используя равносильности, приведенные выше, можно заменить часть формулы или всю формулу равносильной ей формулой. Это преобразование называют равносильным преобразованием данной формулы.
Равносильные преобразования применяются, прежде всего, для упрощения формул. Полученная в результате упрощений формула не должна содержать знаки 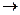 и
и 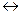 , отрицания неэлементарных формул, например, двойных отрицаний. Она должна содержать меньше, чем исходная, знаков конъюнкции и дизъюнкции.
, отрицания неэлементарных формул, например, двойных отрицаний. Она должна содержать меньше, чем исходная, знаков конъюнкции и дизъюнкции.
Равносильные преобразования формул применяются также для приведения формул к специальному виду или к специальной форме, к так называемой совершенной дизъюнктивной нормальной форме или к совершенной конъюнктивной нормальной форме.
Отметим, что если некоторая формула является тавтологией, то и всякая равносильная ей формула также является тавтологией. Сделанное замечание позволяет обнаружить еще одну сферу применения равносильных преобразований: доказательство тождественной истинности тех или иных формул. Для этого данную формулу нужно равносильными преобразованиями свести к формуле, очевидно являющейся тавтологией.
Пример. Упростить формулу 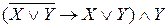 .
.
Запишем последовательность равносильных формул
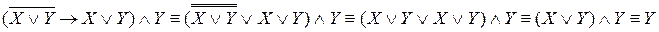
Дата добавления: 2015-08-11; просмотров: 1238;
