Классификация формул алгебры высказываний.
Формула Х называется тождественно истинной (или тавтологией), если она превращается в истинное высказывание, то есть принимает значение 1, при всех наборах значений входящих в нее переменных. Тавтологии представляют собой схемы построения истинных высказываний, независимо от содержания и истинности составляющих элементарных высказываний.
Формула Х называется тождественно ложной, если она принимает значение 0 при всех наборах значений входящих в нее переменных.
Две формулы алгебры логики X и Y называются равносильными, если при любых значениях входящих в них высказывательных переменных логические значения высказываний, получающихся из формул X и Y , совпадают. Для указания равносильности формул используют обозначение 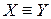 .
.
Существует тесная связь между понятием равносильности формул и понятием тавтологии.
Признак равносильности формул. Две формулы X и Y алгебры высказываний равносильны тогда и только тогда, когда формула 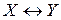 является тавтологией, и обратно, если формула
является тавтологией, и обратно, если формула 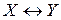 – тавтология, то формулы X и Y равносильны.
– тавтология, то формулы X и Y равносильны.
Отношение равносильности между формулами алгебры высказываний:
а) рефлексивно: 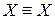 ;
;
б) симметрично: если 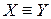 , то
, то 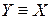 ;
;
в) транзитивно: если 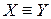 и
и 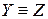 , то
, то 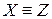 .
.
3.2 Примеры равносильных формул. Равносильности формул алгебры логики часто называют законами логики.
Вот наиболее важные из них:
-
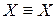 – закон тождества.
– закон тождества. -
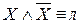 – закон противоречия.
– закон противоречия. -
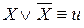 – закон исключенного третьего.
– закон исключенного третьего. -
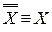 – закон двойного отрицания.
– закон двойного отрицания. -
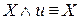 .
. -
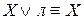 .
. -
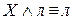 .
. -
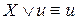 .
. -
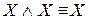 ;
; 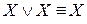 – законы идемпотентности.
– законы идемпотентности. -
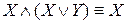 ;
; 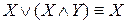 – законы поглощения.
– законы поглощения. -
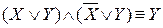 ;
; 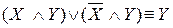 – законы склеивания.
– законы склеивания. - законы коммутативности (переместительности):
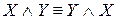 – коммутативность конъюнкции;
– коммутативность конъюнкции;
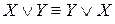 – коммутативность дизъюнкции.
– коммутативность дизъюнкции.
- законы ассоциативности (сочетательности):
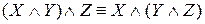 – ассоциативность конъюнкции;
– ассоциативность конъюнкции;
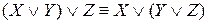 – ассоциативность дизъюнкции.
– ассоциативность дизъюнкции.
- законы дистрибутивности (распределительности):
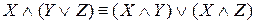 – дистрибутивность конъюнкции относительно дизъюнкции;
– дистрибутивность конъюнкции относительно дизъюнкции;
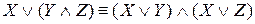 – дистрибутивность дизъюнкции относительно конъюнкции.
– дистрибутивность дизъюнкции относительно конъюнкции.
-
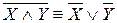 ;
; 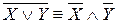 – законы де Моргана.
– законы де Моргана.
Доказать эти равносильности можно, например, с помощью таблиц истинности.
Пример.
Докажем равносильность 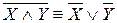 – закон де Моргана. При любых комбинациях значений, от которых зависят формулы X и Y , эти формулы принимают некоторые логические значения. Всего будет четыре способа распределения логических значений X и Y . Надо показать, что в каждом из этих случаев значения левой и правой части равносильности
– закон де Моргана. При любых комбинациях значений, от которых зависят формулы X и Y , эти формулы принимают некоторые логические значения. Всего будет четыре способа распределения логических значений X и Y . Надо показать, что в каждом из этих случаев значения левой и правой части равносильности 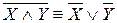 совпадают.
совпадают.
| X | Y | 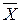
| 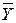
| 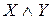
| 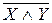
| 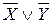
| |
Логические значения в последних двух столбцах совпадают, следовательно, закон де Моргана справедлив.
Имеют место равносильности, выражающие одни логические операции через другие.
Импликациявыражается через:
-
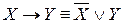 – дизъюнкцию и отрицание;
– дизъюнкцию и отрицание; -
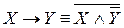 – конъюнкцию и отрицание.
– конъюнкцию и отрицание.
Эквиваленция выражается через:
-
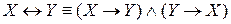 – конъюнкцию и импликацию;
– конъюнкцию и импликацию; -
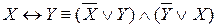 – конъюнкцию, дизъюнкцию и отрицание;
– конъюнкцию, дизъюнкцию и отрицание; -
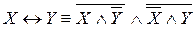 – конъюнкцию и отрицание.
– конъюнкцию и отрицание.
Из этих равносильностей следует вывод, что любую формулу алгебры логики можно заменить равносильной ей формулой, которая будет содержать только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. Дальнейшее исключение логических операций невозможно.
Существует логическая операция, через которую можно выразить любую из пяти логических операций, которыми мы пользуемся: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Эта операция называется «штрих Шеффера», обозначается символом 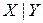 и определяется таблицей истинности
и определяется таблицей истинности
| X | Y | 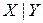
|
Согласно таблице, имеем: 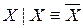 ;
; 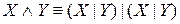 .
.
Дата добавления: 2015-08-11; просмотров: 4354;
