Формулы алгебры логики.
2.1 Формулы алгебры логики.С помощью логических операций над высказываниями из простейших высказываний можно строить высказывания более сложные. При этом порядок выполнения операций указывается скобками. Например, можно построить такое высказывание: «Если Омск находится на берегу Волги и кислород – газ, то 2+3=5». Построенное высказывание символически записывается так: (А /\В)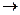 
С. Это высказывание звучит странно, но нас интересует не содержание этого высказывания, а его логическое значение. Логическое значение составного высказывания может быть определено, исходя из логических значений исходных высказываний А, В, С и схемы по которой из исходных высказываний построено сложное высказывание.
Такая схема построения составного высказывания может быть применена к различным конкретным высказываниям, а не только к высказываниям А, В, С . Поэтому ее можно записать в виде (X/\Y) 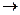Z, где X, Y, Z–некоторые переменные, вместо которых можно подставить любые элементарные высказывания. Переменные, вместо которых можно подставлять любые элементарные высказывания, называют высказывательными или пропозициональными переменными. С помощью высказывательных переменных и символов логических операций любое сложное высказывание можно формализовать, то есть заменить формулой, выражающей его логическую структуру. Эта формула называется формулой алгебры логики.
Теперь сформулируем точное определение формулы алгебры высказываний.
Определение формулы алгебры высказываний.
1. Каждая отдельно взятая пропозициональная переменная есть формула алгебры высказываний.
2. Если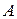 
и 
– формулы алгебры высказываний, то выражения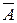 
, 
, 
, 
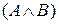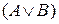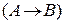и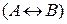 
также являются формулами алгебры высказываний.
3. Никаких других формул алгебры высказываний, кроме получающихся согласно пунктам 1 и 2, нет.
Для составления формулы сложного высказывания нужно:
1) выделить все элементарные высказывания и логические связки, образующие данное составное высказывание;
2) заменить их соответствующими символами;
3) расставить скобки в соответствии со смыслом данного высказывания.
Для упрощения записи формул принят ряд соглашений:
1) скобки можно опускать, если над формулой стоит знак отрицания;
2) можно не заключать в скобки формулы, не являющиеся частями других формул;
3) скобки можно опускать, если придерживаться следующего порядка действий: первой выполняется операция отрицания, затем выполняется конъюнкция, дизъюнкция, импликация и эквиваленция.
Пример.
Формализовать составное высказывание «Две плоскости параллельны тогда и только тогда, когда они не имеют общих точек или совпадают». Выделим и обозначим элементарные высказывания, образующие данное составное высказывание:
А: «Две плоскости параллельны»;
В: «Две плоскости имеют общие точки»;
С: «Две плоскости совпадают».
Тогда данное высказывание в виде формулы записывается так: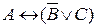 
.
2.2 Таблица истинности.Логическое значение формулы алгебры логики можно определить, если вместо элементарных высказываний вставить символы их логических значений (0 или 1), а затем выполнить над этими символами последовательно все предписываемые формулой операции. Все вероятные логические значения формулы, в зависимости от комбинаций значений входящих в нее переменных, могут быть описаны полностью с помощью таблицы истинности.
Пример. Составить таблицу истинности для формулы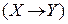 
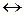
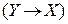. В первых двух столбцах таблицы выпишем всевозможные пары логических значений, которые могут принимать переменные X и Y (точнее, те высказывания, которые могут быть подставлены в формулу вместо переменных X и Y ). В последующих столбцах выписываем логические значения формул 
, 
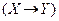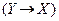и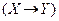 
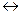
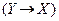, пользуясь определениями логических операций импликации и эквиваленции.
В результате получим таблицу:
| 
| 
| 
| 
| |
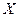
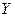
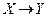
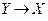
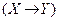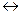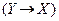
Первые два столбца и последний столбец этой таблицы задают соответствие между логическими значениями элементарных высказываний и логическим значением составного высказывания, получаемого по данной формуле. Эти три столбца образуют таблицу истинности данной формулы. Остальные два столбца, для логических значени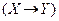й и 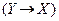, носят вспомогательный, промежуточный, характер.
Если формула содержит n элементарных высказываний, то таблица содержит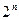 
строк.
Дата добавления: 2015-08-11; просмотров: 3355;