Эквиваленция.

Эквиваленцией (или эквивалентностью) двух высказы­ваний, А и В, называется новое высказывание, которое истинно в том и только в том случае, когда одновременно оба высказыва­ния, А и В, либо истинны, либо ложны, а в остальных слу­чаях – ложно. Эквиваленция высказываний А, В обозначается 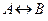и читается «А эквивалентно В», или «для того, чтобы А, необходимо и достаточно, чтобы В», или «А тогда и только тогда, когда В», или «А равносильно В». Высказывания А, В называются членами эквиваленции. Логические значения высказывания 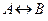, связанные с логическими значениями высказываний А и В, описываются таблицей, называемой таблицей истинности опе­рации эквиваленции:

А	В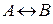

Примеры.

1. Для высказываний «Омск находится на берегу Волги», «2<3» их эквиваленцией будет высказывание «Омск находится на берегу Волги тогда и только тогда, когда 2<3». Так как высказывание «Омск находится на берегу Волги» ложно, а высказывание «2<3» истинно, то составное высказывание на основании определения эквиваленции ложно.

2. Для высказываний «9 делится на 4», «9 делится на 7» их эквиваленцией будет высказывание «9 делится на 4 тогда и только тогда, когда 9 делится на 7». Оба высказывания, к которым применяется связка «тогда и только тогда, когда», ложны. Поэтому все составное высказывание на основании определения эквиваленции истинно.