Резонанс токов

Резонанс токов возникает в цепи с параллельным включением элементов (рис.5.1). Такая цепь содержит два сложных потенциальных узла, а все элементы находятся под одним и тем же напряжением

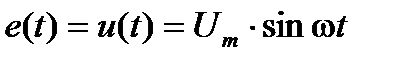. (6.1)

Для любого из узлов - 1 или 1’ справедлив первый закон Кирхгофа:

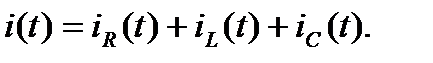(6.2)

Применяя к (5.2) выражения (1.7) и (1.12) приведем его к виду

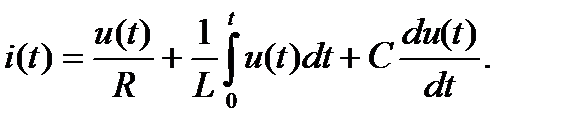(6.3)

Подставим в (5.3) вместо u(t) его значение из (5.1) и решим его

(6.4)

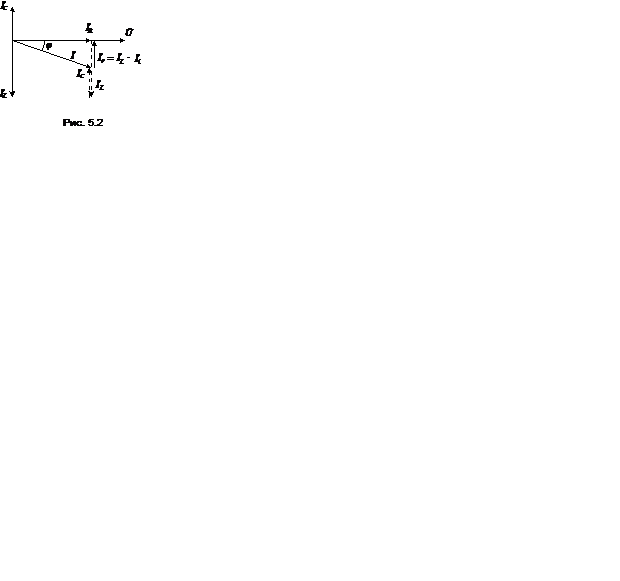
Векторная диаграмма, построенная по (5.4) приведена на рис. 5.2. В качестве исходного в ней принят общий для всех элементов цепи вектор напряжения . С этим вектором совпадает по направлению вектор тока через резистор. Его величина равна

.

Вектор тока через индуктивность 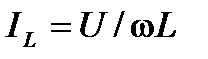отстает от вектора напряжения, а вектор тока через емкость опережает его на 90^о. Проведем последовательное сложение векторов 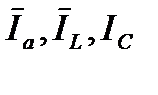. Результатом сложения является вектор 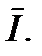Он сдвинут по фазе относительно вектора на угол j. Разность векторов 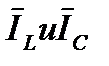дает вектор реактивного тока 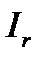. Его величина

. (6.5)

Векторы 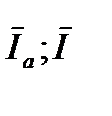и 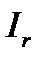образуют треугольник токов. Для этого треугольника справедливы выражения

(6.6)

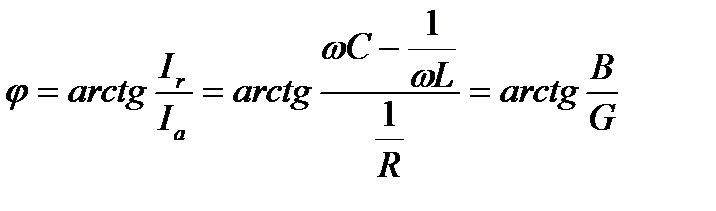. (6.7)

Треугольник токов наглядно показывает, что для достижения резонанса в цепи необходимо обеспечить равенства противофазных токов 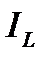и 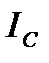. Тогда результирующий реактивный ток цепи 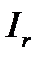и угол j будут равны нулю, а сопротивление цепи станет активным. Из выражения (6.5) видно что может быть равно нулю при соблюдении условия

. (6.8)

Отсюда легко определить:

-частоту 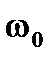, на которой наступает резонанс (резонансную частоту) при заданных значениях элементов L и С

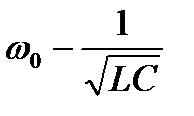; (6.9)

-значение одного из элементов L или С, если заданы резонансная частота 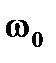и другой элемент

. (6.10)

Определим значение тока всей цепи и токов, протекающих в ее ветвях в режиме резонанса.

Действующее значение тока всей цепи 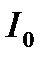на частоте легко найти по (6.6)

(6.11)

Но это значение равно току, протекающему через активное сопротивление цепи 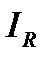т.е.

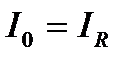(6.12)

Ток, протекающий через элемент L определим по закону Ома

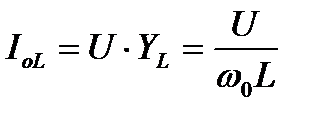. (6.13)

Подставляя в (6.13) вместо U его значение из (6.11) получим

(6.14)

Аналогично определяем выражение для тока через элемент

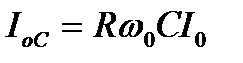(6.15)

Принимая во внимание (6.8) нетрудно сделать вывод о том, что токи, протекающие через индуктивный и емкостной элементы, равны по величине, но противоположны по фазе. Величина Q равная

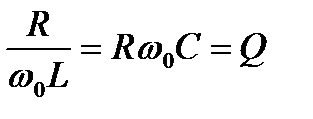(6.16)

может быть больше единицы, в специальных устройствах достигает несколько десятков и сотен единиц и называется добротностью.

Еще раз подчеркнем замечательную особенность цепи в режиме резонанса. Токи протекающие в ветвях реактивных элементов могут принимать значения в десятки и сотни раз больше общего тока цепи. Поэтому резонанс цепи называют резонансом токов. Очень важно и то, что они противофазны. Именно это указывает на то, что в цепи происходит колебательный процесс с частотой по передаче электрической энергии конденсатора в магнитную энергию индуктивности и наоборот. Энергия источника на этот процесс не затрачивается (при идеальных L и С). Она расходуется только на преодоление сопротивления резистора R. Поэтому цепь рис.5.1. называют параллельным колебательным контуром.

Чтобы завершить анализ цепи рассмотрим зависимость ее токов и напряжения от частоты (рис.5.4). Ток, протекающий через элемент R - i_R

определяется законом Ома и не зависит от частоты. Ток через емкость i_c согласно (5.15) прямо пропорционален частоте, а ток через индуктивность i_L –обратно пропорционален. На частоте 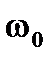они равны по величине, но противоположны по направлению. Общий ток цепи определяется суммой трех токов. Поэтому он имеет большое значение на частотах, дальних от резонансной, но принимает значение i_R на резонансной частоте. Физически это означает что на резонансной частоте проводимость цепи минимальна ( она равна проводимости только элемента R). Поэтому падение напряжения между узлами 1-1’ максимально на частоте и имеет вид резонансной огибающей. В силу этих качеств параллельный колебательный контур широко применяют в радио и радиотехнических устройствах для выделения сигналов на заданной частоте.