Для описания свойств реальных газов

Удивительно, что при всей простоте уравнения Ван-дер-Ваальса, оно дает ясное, качественно правильное описание превращений в системе жидкость-газ. Однако в количественном отношении предсказания на его основе отклоняются от экспериментальных результатов:

• Исходное положение о том, что параметры a и b являются константами для каждого вещества, не оправдалось. Установлено, что они зависят от температуры.

• Полученное значение критического параметра меньше чем экспериментальное значение 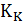для различных веществ. Уравнение Ван-дер-Ваальса лучше описывает легкие газы, чем тяжелые.

• Соотношение 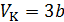не выполняется. Более точным соотношением является соотношение .

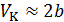• В области сильно сжатых газов и жидкостей, включая область двухфазных состояний, уравнение Ван-дер-Ваальса не имеет теоретического обоснования и приводит к значительным количественным расхождениям с опытом.

14.3. Внутренняя энергия газа Ван-дер-Ваальса

Внутренняя энергия газа может быть представлена суммой кинетической энергии молекул, зависящей от температуры, и потенциальной энергии взаимного притяжения частиц. Если предположить, что теплоемкость 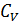не зависит от температуры, то первое слагаемой будет равно .

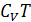Мерой потенциальной энергии притяжения является работа (с противоположным знаком), которую надо затратить для того, чтобы развести молекулы на бесконечно большое расстояние друг от друга. Молярную работу против сил внутреннего давления газа рассчитаем как макроскопическую работу

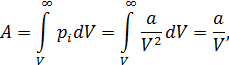
соответственно

Таким образом, внутренняя энергия одного моля газа Ван-дер-Ваальса определяется формулой

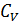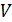где и – молярные величины.

Выражение для энергии (14.11) можно получить и чисто термодинамическим методом согласно (12.25) на основе термического уравнения состояния газа (14.1). Для 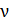молей газа калорическое уравнение состояния имеет следующий вид

Отметим, что полученные выражения для энергии газа Ван-дер-Ваальса справедливы только для физически однородного вещества. Для двухфазных состояний они не применимы. Хотя иногда используются для количественных оценок некоторых параметров.

Анализ формул (14.11) и (14.12) показывает, что при расширении газа в вакуум в условиях адиабатической изоляции, он охлаждается. Подобное явление не может произойти в идеальном газе.

В реальном газе это происходит потому, что хотя газ и не совершает работу против внешних сил. Он совершает работу против внутренних сил молекулярного притяжения за счет уменьшения средней кинетической энергии частиц. Вследствие этого температура газа понижается.

14.4. Эффект Джоуля-Томсона

Основные определения

Многолетние совместные исследования Джоуля и В.Томсона (с 1852 по 1862 гг.) позволили им не только экспериментально подтвердить зависимость внутренней энергии реального газа от его объема. Было открыто важное физическое явление, получившее название эффекта Джоуля-Томсона.

Явление заключается в изменении температуры реального газа при его медленном протекании через пористую перегородку (пробку) в условиях адиабатической изоляции. Стационарное течение газа через пробку называется процессом Джоуля-Томсона, а изменение температуры газа при таком течении дифференциальным эффектом Джоуля-Томсона. Наряду с дифференциальным эффектом существует также интегральный эффект Джоуля-Томсона. Интегральный эффект наблюдается в процессе дросселирования газа, т.е. протекания его через вентиль (малое отверстие), по разные стороны которого давление отличается на несколько порядков, т.е. в сотни или тысячи раз.

Если газ при расширении охлаждается 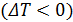, то эффект Джоуля-Томсона называется положительным, а если газ при расширении нагревается 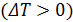, то эффект называется отрицательным. Определения положительного и отрицательного эффектов относятся, как к дифференциальному, так и к интегральному эффекту Джоуля-Томсона.

Описание процесса Джоуля-Томсона

В опыте используется теплоизолированная трубка, разделенная посередине пористой перегородкой, например, пробкой из ваты. По обе стороны пробки находится реальный газ (рис. 14.2). Под действием разности давлений, создаваемой с помощью поршней П₁ и П₂, исследуемый газ медленно протекает через пробку из одной части трубки в другую. Давление газа 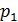и 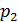по разным сторонам пробки поддерживаются постоянными.

Рис. 14.2.

Несмотря на медленность течения, этот процесс необратим, так как система в целом не является равновесной. Энтропия в изолированной системе возрастает.

Попробуем разобраться, какая функция состояния в этом процессе остается неизменной. Пусть один моль газа при давлении 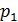(до пробки) занимает объем 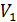. Для того, чтобы переместить этот газ через пробку надо затратить работу внешних сил 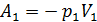. Расширяясь после прохождения пробки до объема 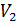при давлении 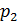, сам газ совершает работу .

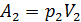Запишем уравнение первого начала термодинамики применительно к рассматриваемому процессу с учетом наличия теплоизолирующей оболочки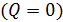

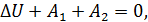
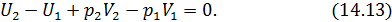
или, что, то же самое,

Посмотрите внимательно на выражение (14.14). Узнаёте? Конечно, здесь написано, что энтальпия «до того» равно энтальпии «после того». Таким образом, в процессе Джоуля-Томсона

Полученное условие постоянства энтальпии является принципиально важным для вычисления эффекта Джоуля-Томсона.

Сущность эффекта Джоуля-Томсона

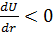Природу этого эффекта можно понять на основе анализа зависимости потенциала межмолекулярного взаимодействия от расстояния между частицами (рис. 13.2). Наличие минимума на кривой Леннарда-Джонса указывает на то, что слева от производная , правее .

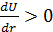Поскольку сумма потенциальной энергии взаимодействия и кинетической энергии величина постоянная, то получаем простое соотношение

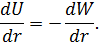
Теперь рассмотрим два случая.

1. Пусть температура газа и его плотность 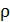настолько велики, что среднее расстояние между молекулами меньше чем : 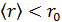. Тогд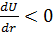а

, а 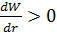, это значит, что кинетическая энергия газа при расширении увеличивается, т.е. его температура повышается. В этом и заключается суть отрицательного эффекта Джоуля-Томсона.

2. Пусть температура газа и его плотность 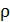настолько низки, что 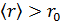. Тогд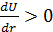а

, а 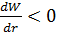, следовательно, кинетическая энергия газа при расширении уменьшается, т.е. его температура понижается. Наблюдается положительный эффект Джоуля-Томсона.

Следовательно, один и тот же газ при одних условиях ( , 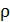– «велики») будет после протекания через пробку нагреваться, а при других условиях ( , 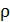– «малы») – охлаждаться. Из приведенных рассуждений также очевидно, что в идеальном газе эффект Джоуля-Томсона невозможен.

Расчет дифференциального эффекта Джоуля-Томсона

Получим формулу эффекта Джоуля-Томсона методом термодинамических потенциалов. Выберем в качестве независимых переменных и 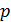и запишем условие (14.15) в дифференциальной форме

Сделаем замену

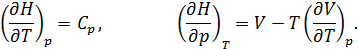
Последнее равенство получается из (12.10) и соотношения Максвелла, имеющего вид

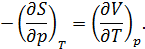
Окончательно из (14.16) получаем

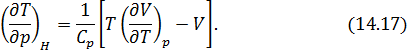
Это и есть искомая формула для дифференциального эффекта Джоуля-Томсона.

Температура, при которой 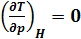, т.е. происходит изменение знака эффекта Джоуля-Томсона, называется температурой инверсии.

Вычисление величины эффекта по формуле (14.17) неизбежно связано с вычислением производной 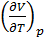, что требует знания термического уравнения состояния исследуемого реального газа. При вычислении эффекта в разреженном газе Ван-дер-Ваальса получается следующее выражение

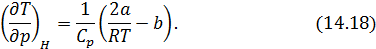
Приравняв к нулю правую часть (14.18), получим температуру инверсии газа Ван-дер-Ваальса:

Температура инверсии определяется индивидуальными параметрами исследуемого газа. Если температура газа больше чем 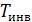, то газ при расширении нагревается (отрицательный эффект), а если его 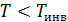, то газ охлаждается (положительный эффект).

Для большинства газов 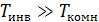. Например, для кислорода 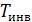=1063 K, для углекислого газа 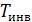= 2073 K. Поэтому, если начальная температура газов равна комнатной 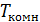, то для них наблюдается положительный эффект: газы охлаждаются.

Для таких газов как водород и гелий . Для водорода 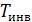= 200 K. Эти газы в процессе Джоуля – Томсона при начальной комнатной температуре нагреваются (отрицательный эффект). Заметим, что в дифференциальном эффекте изменение температуры для обычных газов составляет сотые или десятые доли K. В связи с этим измерение эффекта представляет не простую экспериментальную задачу.

Расчет интегрального эффекта Джоуля-Томсона

Процесс дросселирования газа не является равновесным процессом. Однако начальное и конечное состояния газа являются равновесными и полностью определяются заданием энтальпии и давления. При вычислении изменения температуры реального процесса его заменяют идеальным квазистатическим процессом, происходящим при постоянной энтальпии. Другими словами, интегральный эффект Джоуля-Томсона представляют непрерывной последовательностью дифференциальных эффектов. При таком подходе получаем выражение

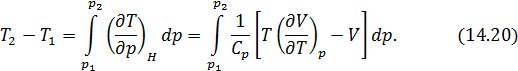
Это и есть формула интегрального эффекта. В ряде случаев интегральный эффект можно рассчитать непосредственно на основе условия (14.15).

Запишем энтальпию газа Ван-дер-Ваальса до дросселирования и после него и приравняем эти величины: 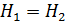. Будем полагать, что после дросселирования к газу применима модель идеального газа, тогда

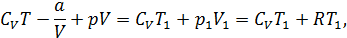
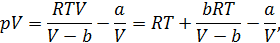
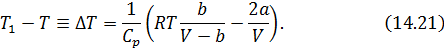
Формула (14.21) описывает интегральный эффект для газа Ван-дер-Ваальса. Из условия 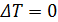, получим выражение для температуры инверсии

Кривая инверсии изображена на рис. 14.3. Как видно с увеличением плотности газа 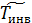уменьшается

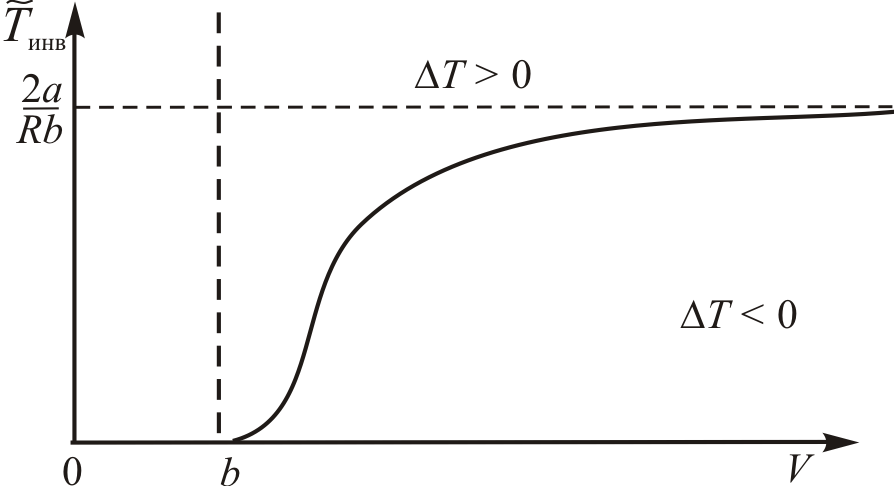
Рис. 14.3.

У достаточно разреженного газа температура инверсии равна 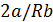, что совпадает с 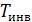дифференциального эффекта. Поведение кривой инверсии (рис. 14.3) характерно для всех реальных газов, это следует из закона соответственных состояний.

Величина интегрального эффекта может достигать десятков и сотен 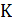. Так, дросселирование водорода может привести к сильному нагреванию газа, в некоторых случаях даже сопровождающемуся взрывом баллона или трубы. А вот дросселирование углекислого газа приводит к такому понижению его температуры, что он при атмосферном давлении переходит в твердое агрегатное состояние – сухой лед.

Интегральный эффект Джоуля-Томсона имеет очень важное практическое значение: наряду с адиабатическим расширением этот эффект используется для получения низких температур.

14.5. Методы получения низких температур

Формирование представлений о низких температурах, их получение и измерение относится к началу XVIII века. Однако прошло почти два века прежде чем низкие температуры стали мощным инструментом исследования вещества. Началом физики низких температур как раздела физики, изучающего свойства вещества и процессы при температурах вблизи абсолютного нуля, следует считать 1908 год. Именно в этом году в Лейденской криогенной лаборатории под руководством Х.Камерлинг-Оннеса было осуществлено сжижение гелия и началось исследование свойств различных веществ при гелиевых температурах (4,2 ÷ 1 ).

К настоящему времени в физике сложилась следующее подразделение основных температурных диапазонов:

1. Криогенные температуры – Т < 80 .

2. Низкие температуры – Т < 0,3 .

3. Сверхнизкие температуры – 10^-3 ÷10^-6 и ниже.

На схеме 14.5.1. представлены методы получения криогенных температур в различных интервалах.

Схема14.5.1.

Интервал температур, K

Физические основы методов

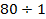
Адиабатическое расширение и эффект Джоуля-Томсона

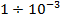
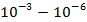и ниже

Растворение жидкого 3He в жидком гелии 4He(поглощается теплота растворения)

Метод адиабатического размагничивания парамагнитных атомов и ядерных спинов.

Широкий спектр проблем получения криогенных температур и способы их решения представлены в книге Петра Леонидовича Капицы [7] в главе «Криогенная техника».

Остановимся более подробно на обсуждении двух наиболее распространенных методах получения криогенных температур.