Метод противоточного обмена теплотой
Рассмотрим в общих чертах способ получения криогенных температур, в основе которого лежат процесс Джоуля-Томсона и адиабатическое расширение газа, а также их комбинация.
Сначала газ изотермически сжимается в компрессоре до давления несколько сотен атмосфер при комнатной температуре. После чего он расширяется либо в процессе Джоуля-Томсона, либо адиабатически. В результате газ охлаждается и используется для предварительного охлаждения следующей порции газа. Эта порция после расширения окажется при температуре более низкой, чем первая. С её помощью охлаждается следующая порция газа и т.д. После многих циклов температура понижается до необходимого значения.
На практике используется метод охлаждения газа путем теплообмена между встречными потоками газа, который так и называется методом противоточного обмена теплотой [7]. Устройство, в котором это происходит, называется теплообменником. Устройство, в котором газ адиабатно расширяется и при этом охлаждается, называется детандером.
Часто газ в состоянии исходного сжатия охлаждают другим сжиженным газом, полученным в другой установке. Например, при производстве жидкого гелия его предварительное охлаждение происходит с помощью жидкого водорода. В свою очередь в производстве жидкого водорода может быть использован жидкий азот.
Температуру ниже температуры кипения жидкого гелия (4,19 
) можно получить уменьшением давления над кипящей жидкостью путем откачки. Предельное значение достигаемой температуры этим методом равно 0,72 . Дальнейшее понижение температуры может дать достигнуто принципиально другими методами.
Метод адиабатического размагничивания
Этот метод основан на зависимости энтропии парамагнитной соли от величины напряженности внешнего магнитного поля, в которое помещен образец. Кроме того используется свойство изоэнтропийности обратимого адиабатного процесса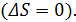 
Представим описание метода в виде последовательности совершаемых действий и получаемых результатов:
• Парамагнитный образец, находящийся в контакте с жидким гелием (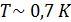 
) поместим в медленно растущее магнитное поле и адиабатически намагнитим его.
• Энтропия системы магнитных моментов ионов соли вследствие их упорядочения во внешнем поле уменьшается: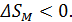 
• При этом увеличивается энтропия, связанная с тепловыми колебаниями кристаллической решетки соли: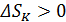 
. Парамагнетик в адиабатном процессе нагревается, поскольку
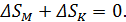
• Парамагнетик в намагниченном состоянии, находясь в контакте с жидким гелием, не изменят свою температуру (0,7 ).
• Устраним контакт образца с жидким гелием.
• Медленно уменьшим внешнее магнитное поле до нуля.
• Парамагнетик размагничивается, хаос в системе магнитных моментов растет: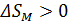 
.
• Это приводит к понижению температуры образца. Вследствие этого энтропия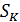 
уменьшается, 
.
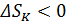Тепловой эффект адиабатного охлаждения весьма велик. Используя для размагничивания несколько граммов квасцов (хромокалиевых или железоаммониевых), можно понизить температуру нескольких килограммов диамагнитного вещества с 1 до сверхнизких температур (~10-3 ). Используя более сложный процесс адиабатного размагничивания ядерных спиновых моментов, можно получить температуры до 10-8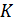 
и ниже.
При криогенных температурах проявляются многие необычные свойства вещества, например, такие как сверхпроводимость и сверхтекучесть.
Контрольные вопросы
1.Какие состояния вещества соответствуют волнообразному участку на изотерме Ван-дер-Ваальса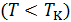 
? При каких условиях эти состояния могут быть реализованы?
2.В каких приборах (устройства) находят применение метастабильные состояния вещества?
3.Какими способами можно найти значения критических параметров? Запишите значения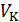 
, 
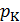и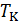 
в приближении Ван-дер-Ваальса.
4.Почему газовая постоянная в критическом состоянии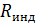 
меньше чем R=8,31 Дж/моль· ?
5.Что называется приведенным уравнением состояния? Сформулируйте закон соответственных состояний.
6.Опишите критические явления.
7.Как проявляются флуктуации плотности вещества в критическом состоянии?
8.Обладая очевидными достоинствами, уравнение Ван-дер-Ваальса не лишено недостатков. Назовите их.
9.Запишите калорическое уравнение состояния газа Ван-дер-Ваальса.
Почему реальный газ при расширении в вакуум охлаждается?
10.Как происходит процесс Джоуля-Томсона? В чем заключается сущность эффекта Джоуля-Томсона?
11.Что называется температурой инверсии? Как эта величина зависит от объема газа в интегральном эффекте Джоуля-Томсона?
12. Объясните суть метода адиабатического размагничивания применяемого для получения сверхнизких температур.
ЛЕКЦИЯ 15
ФАЗОВЫЕ ПЕРЕХОДЫ ПЕРВОГО И ВТОРОГО РОДА
15.1. Условие равновесия фаз химически однородного вещества
Фазовые превращения в системе газ-жидкость, включая переход в критическое состояние, мы рассмотрели в предшествующих двух лекциях. Там же мы дали определение фазы и проиллюстрировали его на примере фаз различных агрегатных состояний вещества.
Однако фазовые переходы могут происходить и без изменения агрегатного состояния. Например, в твердом состоянии некоторые вещества могут существовать в зависимости от температуры и давления в нескольких кристаллических модификациях. Это явление называется полиморфизмом. Графит при давлении более 1,5 ГПа становится алмазом, при этом вещество (углерод) остается в твердом состоянии, изменяется его кристаллическая структура и физические свойства. Подобные превращения называются полиморфными. При температуре около 2 происходит превращение обыкновенного жидкого гелия в другую жидкую модификацию, обладающую свойством сверхтекучести. Постоянный магнит при нагревании выше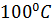 
теряет магнитные свойства, ферромагнетик превращается в парамагнетик. Пришло время расширить и обобщить наши представления о фазах и фазовых переходах.
Различают фазовые переходы первого рода, которые сопровождаются выделением или поглощением теплоты, и второго рода, происходящие без теплообмена.
К фазовым переходам первого рода относятся превращения вещества из одного агрегатного состояния в другое, а также полиморфные превращения в кристаллах. При такого рода превращениях две фазы одновременно существуют в объеме и пространственно разграничено.
Структурные изменения, приводящие к таким свойствам макросистем, как ферромагнетизм, сегнетоэлектричество, сверхтекучесть, сверхпроводимость, как правило, относят к фазовым переходам второго рода. Фазовые переходы второго рода происходят сразу во всем объеме и обязательно сопровождаются изменением симметрии системы.
При равновесном переходе химически однородного вещества из одной фазы в другую, как и при фазовом равновесии, температура и давление всех фаз одинаковы. Обозначим различные фазы многофазной системы буквам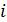и 
и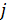 
, тогда первый признак равновесия фаз можно записать
Второй признак равновесия фаз фиксирует то обстоятельство, что равновесие является не статическим, а динамическим или статистическим. На границе раздела фаз происходит непрерывный обмен молекулами между этими фазами и средняя скорость превращения фазы 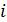в фазу 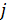равна средней скорости превращения фазы 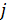в фазу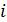
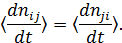
Третий признак – это условие устойчивости термодинамического равновесия закрытой системы, есл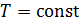и 
и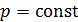 
. Устойчивость в этом случае определяется минимумом термодинамического потенциала Гиббса
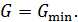
Условие динамического равновесия фаз, отвечающее этим трем признакам, выражается уравнением
где 
, 
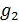– удельные термодинамические потенциалы i-й и j-й фаз соответственно. Поясним суть условия (15.4) на примере двухфазной системы. Её полный термодинамический потенциал имеет вид
где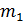 
и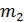 
- массы первой и второй фазы соответственно. Пусть давление и температура системы поддерживаются постоянными. Тогда при фазовых превращениях величины и 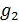не будут меняться, так они являются однозначными функциями температуры и давления. Полная масса системы не изменяется 
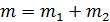, но будут изменяться массы 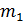и 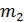, причем так, чтобы обеспечить наименьшее значение 
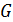, какое только возможно, в данных условиях. Если 
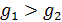, то фаза 1 превратится в более устойчивую фазу 2. Вся система станет однофазной, 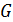достигнет минимального значения 
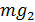. В случае, если 
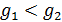, фаза 1 в итоге превратится в фазу 1, обеспечив тем самым минимальное значение 
.
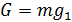Таким образом, условием равновесия фаз является равенство их удельных термодинамических потенциалов (15.4). Другая формулировка этого условия гласит, что при любых фазовых превращениях величина удельного термодинамического потенциала всегда изменяется непрерывно.
15.2. Классификация фазовых переходов по Эренфесту
Многочисленные экспериментальные исследования показали, что все фазовые превращения сопровождаются скачкообразными изменениями каких-либо макроскопических величин, характеризующих свойства вещества. При теоретическом рассмотрении выяснилось, что эти параметры могут быть выражены через частные производные первого и второго порядка от удельного термодинамического потенциала Гиббса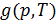 
.
Это обстоятельство было положено в основу классификации фазовых переходов, предложенной П.Эренфестом в 1933 году.
Фазовые переходы, при которых первые производные удельного термодинамического потенциала 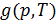меняются скачкообразно, называются фазовыми переходами первого рода.
Фазовые переходы, при которых первые производные функции 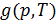остаются непрерывными, а вторые производные меняются скачкообразно, называются фазовыми переходами второго рода.
Как уже отмечалось, за каждой абстрактной производной термодинамического потенциала Гиббса стоит хорошо измеряемый макроскопический параметр вещества. Проследим, как проявляется это соответствие для фазовых переходов первого и второго рода.
Фазовые переходы первого рода
Согласно уравнениям (12.22) и (12.23)
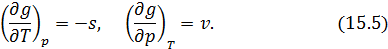
Поэтому фазовые превращения первого рода сопровождаются скачкообразными изменениями либо удельной энтропии 
, либо удельного объема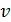 
, либо обеих этих величин вместе. Скачок удельной энтропии означает, что фазовый переход происходит с выделением или поглощением количества теплоты 
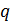. Сама величина скачка удельной энтропии равна
где 
– температура фазового перехода. В зависимости от вида фазового превращения удельную теплоту фазового перехода называют либо теплотой кристаллизации, либо теплотой возгонки, либо теплотой испарения и т.п. Скачок удельного объема 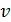означает, что плотности разных фаз вещества различаются между собой: 
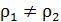. В литературе фазовые переходы первого рода называются так же прерывными превращениями [1].
Фазовые переходы второго рода
При фазовых превращениях второго рода претерпевают разрыв все или некоторые вторые производные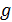 
, такие как
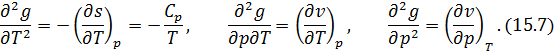
Каждой из этих производных соответствует физическая величина, которая может меняться скачком, при фазовом переходе второго рода, это
• удельная теплоемкость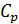 
;
• термический коэффициент объемного расширения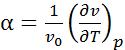 
;
• термический коэффициент сжатия вещества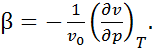 
В литературе фазовые переходы второго рода называются также непрерывными превращениями или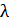 
- переходами Последнее название появилось потому, что в окрестности температуры фазового перехода график зависимости удельной теплоемкости 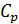от температуры напоминает греческую букву 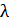. Температуру непрерывного фазового перехода, зависящую от давления, называют 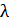-точкой или точкой Кюри.
Точкой Кюри обычно называют температуру превращения ферромагнетика в парамагнетик, сегнетоэлектрика в диэлектрик, сверхпроводника в проводник. Перечисленные переходы изучаются в курсе «Электричество и магнетизм». Теория фазовых переходов второго рода до настоящего времени находится в стадии разработки, в ней ещё достаточно «белых» пятен. В качестве примера непрерывного перехода мы рассмотрим в 15.5 сверхтекучий переход в жидком гелии. Ближайшее рассмотрение вопросов будет ограничено фазовыми переходами первого рода.
15.3. Фазовые переходы первого рода. Диаграмма состояний
Рассмотрим систему, состоящую из трех фаз: твердой, жидкой и газообразной. Индексом 1 обозначим газ, а индексами 2 и 3 жидкую и твердую фазы. Для фазового равновесия требуется выполнение трех условий:
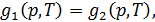
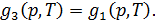
Эти условия не независимы. Каждое из них является следствием двух других. Графическое решение каждого из уравнений (15.8) соответствует кривой двухфазного термодинамического равновесия на плоскости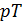 
(рис. 15.1).
Первое уравнение системы определяет кривую равновесия между газом и жидкостью, т.е. кривую испарения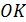 
(рис. 15.1). Второе уравнение дает кривую равновесия жидкости и твердого тела 
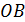, называемой кривой плавления. Кривая плавления пересекается с кривой испарения в точке 
, которая называется тройной точкой, потому что через неё проходит и третья
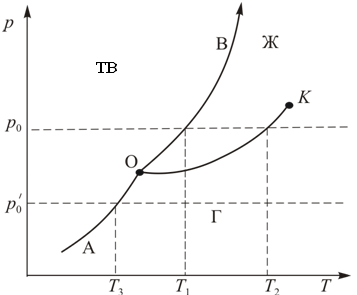
Рис.15.1.
кривая равновесия – кривая возгонки, или сублимации, 
. Третья кривая соответствует равновесию твердой и газообразной фаз.
Таким образом, три фазы могут находиться в равновесии друг с другом лишь в одной, а именно, тройной точке при определенных значениях температуры и давления. Плоскость 
с представленными на ней кривыми равновесия многофазной системы, называется диаграммой состояния или фазовой диаграммой.
Кривые равновесия делят плоскость диаграммы состояния на области существования каждой из трех фаз: твердой (ТВ), жидкой (Ж) и газообразной (Г). В точке (критической точке)исчезает различие между свойствами жидкости и газа. Таким образом, любая точка фазовой диаграммы изображает равновесное состояние вещества при данных значениях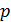 
и , но только точки кривых равновесия соответствуют сосуществованию двух фаз.
Диаграмма состояния позволяет судить, какие будут происходить фазовые превращения при различных процессах. Например, процесс изобарического нагревания на диаграмме состояния представляется горизонтальной прямой. Если изобара проходит выше тройной точки, но ниже критической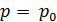 
(рис. 15.1). то её пересечение с двумя кривыми равновесия определяет два фазовых перехода. Значит, при нагревании твердое тело сначала расплавится при температуре 
, а затем при температуре 
жидкость испарится. Если же изобара проходит ниже тройной точки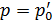 
(рис. 15.1), то она пересекает только кривую возгонки. Поэтому при температуре 
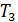произойдет непосредственное превращение твердого тела в газообразное состояние.
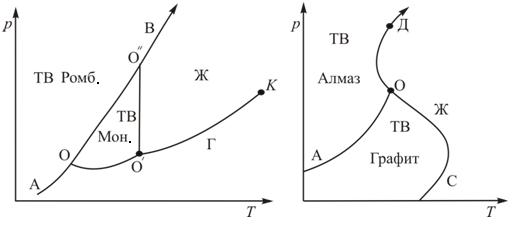
Если число фаз, в которых может находиться химически однородное вещество при различных давлениях и температурах, больше трех, то все равновесные состояния системы также можно изобразить на фазовой диаграмме. Только следует иметь в виду, что максимальное число фаз, находящихся в равновесии друг с другом, не может превышать трех.Поэтому на диаграмме состояний появится несколько тройных точек, но ни одной «четверной» или «шестерной» точки на ней быть не может. В качестве примеров на рис. 15.2. представлены в упрощенном виде диаграммы состояний серы (а) и углерода (б).
а б
Рис.15.2.
Сера может существовать в двух кристаллических модификациях - моноклинной и ромбической. Поэтому на диаграмме состояния (15.2. а) имеются три тройных точки 
именно 
. Область моноклинной модификации ограничена треугольником 
. Область ромбической модификации лежит выше кривой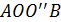 
. Проводя горизонтальные прямые – изобары, пересекающие кривые равновесия, можно предсказать все возможные фазовые переходы и их температуры и давления.
На рис. 15.2. б дана диаграмма состояния углерода, у которого существуют две устойчивые модификации – графит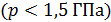 
и алмаз 
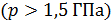. Алмаз может существовать, и как нам известно, прекрасно существует и при более низких давлениях вплоть до атмосферного. В этом случае его состояние является метастабильным, хотя оно и очень устойчиво. Алмаз в нем может находиться достаточно долго и лишь при нагревании до 103 переходит в графит. Аналогичное упрямство проявляет и графит, и он не переходит в алмаз, хотя его температура и давление доведены до соответствующих значений. Превращение графита в алмаз в своё время было сложной научно-технической задачей. Эта задача была успешно решена, после чего стало возможным промышленное производство искусственных алмазов.
Завершая анализ диаграмм состояния отметим, что поскольку кривая испарения заканчивается в критической точке, то её можно обойти сверху без пересечения кривой испарения и перевести газ в жидкость минуя двухфазное состояние. Подобный непрерывный переход возможен и в обратном направлении. Это связано с тем, что различие между газом и жидкостью является чисто количественным. Они отличаются величиной энергии межатомных взаимодействий. Однако оба состояния изотропны и характеризуются одинаковой симметрией (точнее хаосом) внутренней структуры. Различия между жидкостью (газом) и твердым телом или двумя модификациями твердого тела носят совершенно иной характер. Отличия имеют не только количественный, но и качественный характер. Симметрия внутреннего строения этих фаз различна и она может измениться только скачком. Поэтому кривые плавления и возгонки не могут обрываться в изолированной точке. Они могут либо заканчиваться в точке пересечения её с другой кривой равновесия (рис. 15. а), либо уходить в бесконечность.
15.4. Уравнение Клапейрона-Клаузиуса
Рассматривая диаграммы состояний разных веществ, мы обращаем внимание на то, что кривые фазового равновесия имеют разную крутизну, или наклон. Тангенс наклона фазовой кривой равен производной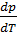 
.
Спрашивается, от чего зависит эта производная? Через какие макроскопические параметры выражается наклон кривой фазового равновесия? Ответ на эти вопросы даёт уравнение Клапейрона-Клаузиуса. Это уравнение может быть получено, по крайней мере, двумя способами. Первый способ – это метод термодинамического потенциала, а второй – метод циклов.
Вывод уравнения Клапейрона-Клаузиуса
методом термодинамического потенциала
Описание системы и процесса
Исследуется двухфазная система. Устойчивое равновесие фаз описывается зависимостью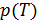 
вдоль кривой фазового равновесия. Эта зависимость неизвестна. Для определенности рассмотрим кривую испарения.
Актуальные свойства процесса
При смещении вдоль кривой испарения справедливо равенство (15.4). В дифференциальной форме оно имеет вид
где индексы 1 и 2 соответствуют газообразной и жидкой фазам.
Постановка задачи
Требуется получить выражение для производной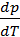 
вдоль кривой испарения.
Вывод уравнения
• Запишем бесконечно малое изменение удельного термодинамического потенциала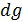 
:
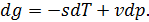
• Используя это выражение, перепишем (15.9):
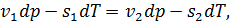
или
Равенство (15.10) называется уравнением Клапейрона-Клаузиуса. Как видно производная 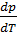определяется отношением скачкообразного изменения удельной энтропии к величине скачкообразного изменения удельного объема при испарении. Скачок удельной энтропии в (15.10) можно выразить согласно (15.6). Тогда уравнение Клапейрона-Клаузиуса примет свой наиболее известный вид:
Вывод уравнения Клапейрона-Клаузиуса методом циклов
Рассматривается бесконечно малый цикл Карно, который осуществляется с двухфазной системой, состоящей из жидкости и её насыщенного пара. Масса системы равна одному килограмму.
Актуальные свойства процесса
• Давление насыщенного газа однозначно определяется его температурой.
• Изотерма 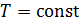является в то же время изобарой .
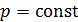• Температуры изотерм в цикле Карно отличаются на бесконечно малую величину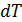 
.
Постановка задачи
Требуется получить выражение для производной вдоль кривой испарения.
Вывод уравнения
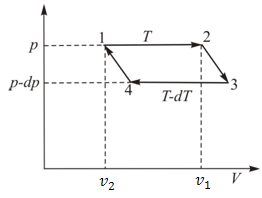Совершаемый с системой цикл Карно изображен на рис. 15.3.
• Как видно из рисунка работа , совершенная за цикл, равна площади, ограниченной параллелограммом 1-2-3-4 на диаграмме 
.
• Эту работу нетрудно подсчитать
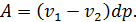
| Рис. 15.3. |
• Количество теплоты, поступившее в систему от нагревателя за цикл, равно удельной теплоте испарения q.
• Запишем КПД для цикла Карно через температуры холодильника и нагревателя и через отношение совершенной системой работы к поступившему в систему количеству теплоты и приравняем эти выражения
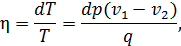
• Из этого уравнения следует
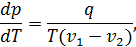
что, конечно, совпадает с уравнением (15.11).
Уравнение Клапейрона-Клаузиуса справедливо не только для испарения, но и для всех фазовых превращений первого рода, поскольку только они сопровождаются выделением или поглощением скрытой теплоты перехода.
В случае плавления можно записать
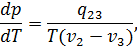
где 
– удельная теплота плавления, 
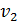и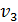 
- удельные объемы жидкой и твердой фаз, – температура плавления при давлении 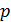. Величина положительна, поэтому, если 
, то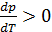 
. Именно такой ход кривых фазового равновесия представлен на рис. 15.1, 15.2. Если же 
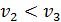, то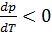 
, т.е. при увеличении давления температура плавления понижается. Вещества, для которых выполняется последнее условие, называются аномальными. К ним относятся висмут и сурьма, а также вода (лед) при атмосферном давлении.
15.5. Диаграмма состояний гелия. Сверхтекучесть жидкого гелия.
Сверхтекучесть жидкого гелия была открыта и изучена в 1938 году П.Л. Капицей. Квантовую теорию эффекта в 1941 году предложил Л.Д. Ландау. За открытие этого явления и создание его теории Капица (1978) и Ландау (1962) были удостоены Нобелевской премии по физике.
Вы уже знаете. Что жидкий гелий существует в области не только низких, но и сверхнизких температур, сколь угодно близких к 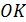. Таким образом, гелий – самая холодная жидкость в природе. В экспериментальной физике гелий используется при многих исследованиях, требующих низких температур. Особенно важно использование гелия при исследовании сверхпроводимости и создания условий для эксплуатации сверхпроводящих магнитов. Ярким примером использования жидкого гелия служит система Большого адронного коллайдера, созданного международным проектом ЦЕРНа. Для удержания пучков протонов, разгоняемых до почти световой скорости в 27-километровом кольце ускорителя нужны настолько мощные магниты, которые могут быть созданы лишь из сверхпроводников. Рабочая температура магнитов составляет около 1,9 и поэтому может быть достигнута только в контакте с жидким гелием. Диаграмма состояний гелия представлена на рис. 15.4.
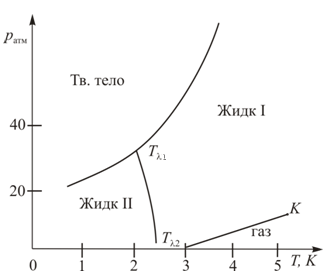
Рис.15.4.
Гелий может существовать в газообразной, твердой и двух жидких модификациях:
I и II. Обращает внимание отсутствие на диаграмме состояний гелия кривой возгонки. Если охлаждать жидкий гелий II, то при определенной температуре (зависящей от внешнего давления) он превращается в жидкий гелий II. Этот переход осуществляется по линии 
. Жидкость остается жидкостью, её плотность не меняется 
и отсутствует скрытая теплота перехода. Нет ни одного признака фазового перехода первого рода. Зато обнаруживается скачок теплоемкости в окрестности температуры фазового перехода.
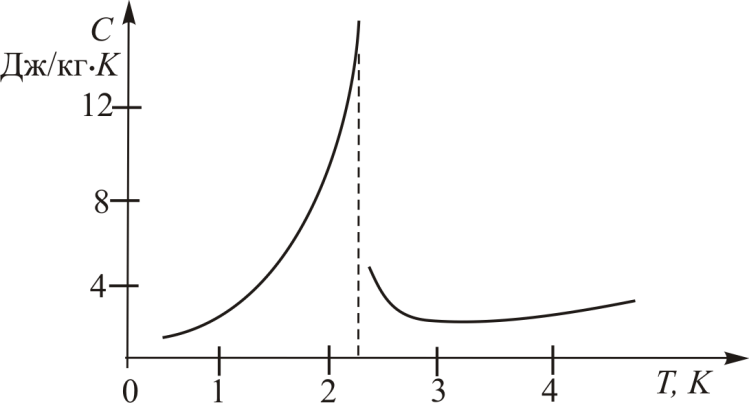
Рис.15.5.
Зависимость 
жидкого гелия приведена на рис. 15.5. Это явный признак 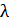-перехода, или перехода второго рода.
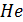II является бесцветной прозрачной жидкостью и не отличается по внешнему виду от 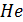I. Единственное внешнее отличие наблюдается в точке кипения при атмосферном давлении. 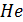I интенсивно кипит по всему объему, в то время как 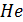II образует спокойную поверхность без образования пузырьков в объеме жидкости. Все превращения жидкости в пар происходят на границе фаз, это является следствием сверхтеплопроводности 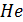II .
Самым важным и поразительным свойством 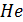II является, конечно же, его сверхтекучесть [7]. Сверхтекучий гелий не обладает вязкостью. Он без трения протекает через узкие капилляры и щели 
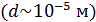. В то же время II оказывает сопротивление движущимся в нем телам. Это кажущееся противоречие находит свое разрешение в следующем обстоятельстве. Оказывается, жидкость состоит из двух компонент – нормальной (вязкой) и сверхтекучей, которые взаимно проникают друг в друга.
При течении через узкий капилляр нормальная компонента покоится относительно стенок сосуда, а сверхтекучая компонента движется без трения. Относительно макроскопических тел движутся обе компоненты, поэтому появляется сила вязкого трения, направленная против направления скорости движения тела.
Плотность жидкого гелия II равна сумме плотностей нормальной и сверхпроводящей компонент
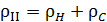
Полная плотность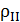 
не зависит от температуры, но её распределение между 
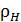и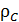 
сильно зависит от температуры. При 
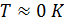существует только сверхтекучая компонента, при температуре 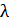-перехода - только нормальная компонента. Поэтому на линии 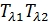сверхтекучесть исчезает.
Свойство сверхтекучести проявляется лишь при достаточно малых скоростях течения, не превышающих некоторой критической скорости. Сверхтекучесть определяет и сверхтеплопроводность 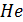II , поскольку передача теплоты в нем осуществляется не в процессе тепловой диффузии (теплопроводности), а конвективными потоками сверхтекучей жидкости. В результате теплопроводность гелия в сотни раз превышает теплопроводность серебра.
Гелий II обладает еще целым рядом интереснейших свойств, с некоторыми из них вы можете познакомиться в [1].
Сверхтекучесть – сугубо квантовое явление, не объясняемое классической физикой. Гелий II – это единственная квантовая жидкость. При теоретическом рассмотрении адекватной моделью материального тела является конденсат идеального газа, подчиняющегося статистике Бозе-Эйнштейна. Обсуждение этой модели выходит за рамки данного курса.
Контрольные вопросы
1. Какие превращения называются полиморфными? Приведите примеры.
2. Приведите примеры фазовых переходов первого и второго рода.
3. Назовите три признака равновесия фаз.
4. Сформулируйте условие равновесия фаз химически однородного вещества.
5. Дайте классификацию фазовых переходов по Эренфесту.
6. Какие свойства вещества могут меняться скачкообразно при фазовых переходах а) первого рода, б) второго рода?
7. Что называется диаграммой состояния? Поясните на рисунке. Какая точка на диаграмме называется тройной точкой? Сколько тройных точек может содержать диаграмма состояния.
8. Какую информацию можно получить с помощью фазовой диаграммы вещества?
9. Почему кривая испарения заканчивается критической точкой, а кривая плавления такой точки не имеет?
10. Запишите уравнение Клапейрона-Клаузиуса, поясните его смысл.
11. Каким способом можно вывести уравнение Клапейрона-Клаузиуса? К каким фазовым превращения оно применимо?
12. Опишите 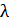-переход в жидком гелии. Как проявляется сверхтекучесть 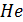II? Какие интересные свойства жидкого гелия вам известны?
ЛЕКЦИЯ 16
ПРОЦЕССЫ ПЕРЕНОСА В РЕАЛЬНЫХ СИСТЕМАХ
16.1. Релаксационные процессы в молекулярных системах
В равновесных системах, изучением которых мы занимались до настоящего времени, температура и другие макроскопические параметры были постоянными во всех частях системы. Если это условие нарушено, то система является неравновесной. Наличие градиентов температуры, концентрации частиц, электрического потенциалов приводит к возникновению потоков энергии, вещества или заряда. Подобные процессы являются необратимыми и называются процессами переноса.
Изолированная система, предоставленная самой себе, будет постепенно переходить к равновесному состоянию. Как вы помните, время, в течение которого система достигает равновесного состояния, называется временем релаксации и обычно обозначается буквой 
. Если отклонение от равновесия происходит по нескольким параметрам, то времена релаксации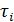 
по этим параметрам различаются между собой. Распределение Максвелла по скоростям мы вывели и применяли для идеального газа, однако оно также справедливо для реальных газов и жидкостей, лишь бы система находилась в термодинамическом равновесии. Время, в течение которого система приходит к распределению Максвелла, называется временем релаксации к распределению Максвелла или временем термализации 
.
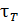Неравновесная смесь нескольких газов придет к распределению Максвелла с разными для каждой компоненты 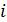временами термализации 
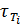. В отсутствие внешних силовых полей, как мы знаем, концентрация частиц постоянна по всему объему, занимаемому системой. Выведенная из равновесия по этому параметру макросистема спустя время релаксации 
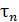вернется к однородному распределению молекул. Однако это время релаксации не равно времени термализации той же системы. Время релаксации для концентрации частиц во внешнем силовом поле, например, в поле тяжести, отличается от времени релаксации для концентрации в отсутствии консервативных сил. Оценка различных времен релаксации имеет большое значение. Процессы с самыми короткими временами релаксации приводят систему очень быстро к состоянию равновесия по этим параметрам и анализ приближения системы к равновесию по оставшимся параметрам существенно упрощается.
Сравнение времен релаксации предполагает, что размер системы фиксирован, имеется в виду её масса, объем, количество частиц. Время релаксации растет с увеличением размеров системы. Самопроизвольный переход отдельных макроскопических малых частей системы в равновесное состояние осуществляется значительно раньше, чем устанавливается равновесие между этими частями.
В термодинамике неравновесных систем исходят из представления о локальном равновесии. Суть его в том, что хотя в целом состояние системы является неравновесным, отдельные её малые части равновесны (квазиравновесны) в том смысле, что термодинамические параметры в этих физически малых частях медленно изменяются во времени и от точки к точке. Размеры этих равновесных областей в неравновесной системе выбираются таким образом, чтобы время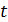 
изменения термодинамических параметров было намного больше времени релаксации в них и намного меньше времени релаксации всей системы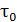 
Исходное положение о локальном равновесии позволяет построить последовательную феноменологическую термодинамику необратимых процессов, рассмотрение которой выходит за рамки этого курса.
Строгая молекулярно-кинетическая теория явлений переноса очень сложна. Она сводится к приближенным решениям, так называемого, кинетического уравнения Больцмана. Уравнение Больцмана – это нестационарное интегро-дифференциальное уравнение для функции распределения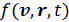 
в неравновесном состоянии. Рассмотрением этого уравнения вы займетесь в курсе «Статистическая физика», после того, как существенно усилите свою математическую подготовку. Мы же ограничимся элементарной теорией явлений переноса, а именно, методом средней длины свободного пробега. Прежде чем обратиться к микроскопической теории, проанализируем процессы переноса в рамках феноменологического похода.
16.2. Стационарные уравнения переноса в газах, жидкостях и твердых телах
Типичными явлениями переноса, если отклонения от равновесия невелики, являются теплопроводность, диффузия (самодиффузия), внутреннее трение, электропроводность. Подобные процессы могут быть стационарными и нестационарными. Ограничимся рассмотрением только стационарных процессов.
Уравнения переноса были получены в XIX веке в рамках феноменологической, а точнее, сугубо математической теории. Все они имеют однотипную структуру, отражающую причинно-следственную связь. В качестве причины рассматривается наличие градиента некоторого макроскопического параметра, следствием же является возникновение потока определенного молекулярного свойства. Реакция системы на внешнее воздействие в конкретных процессах переноса однозначно определяется принципом Ле Шателье-Брауна.
Например, если температура в системе меняется от точки к точке(grad T ≠ 0), то внутри системы возникнет поток энергии и именно в том направлении, чтобы «уменьшить несправедливость» и выровнять температуру во всей системе. Аналогичным образом реагирует система, в которой есть градиент концентрации каких-то молекул, а именно возникновением потока этих молекул, направленного так, чтобы равномерно распределить молекулы по объему занимаемому системой. Конечно, если система неизолированная, то можно поддерживать постоянные значения градиентов макроскопических параметров. Система, разумеется, не сможет перейти в равновесное состояние, но потоки молекулярных свойств будут существовать всё то время, которое будут существовать градиенты параметров.
Рассмотрим стационарные одномерные уравнения теплопроводности, самодиффузии и внутреннего трения.
Уравнение теплопроводности
Уравнение теплопроводности называется уравнением Фурье и имеет вид
где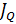 
– плотность потока теплоты (внутренней энергии), 
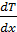– градиент температуры вдоль направления оси 
, 
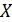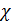– коэффициент теплопроводности (теплопроводность). Размерности входящих в уравнение величин таковы:
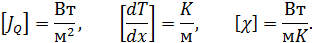
Знак « - » в правой части (16.1) обусловлен тем, что направление плотности потока противоположно градиенту 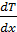(рис. 16.1).
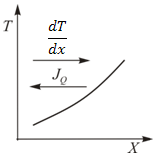
Рис.16.1.
Уравнение самодиффузии
Уравнение самодиффузии называется уравнением Фика:
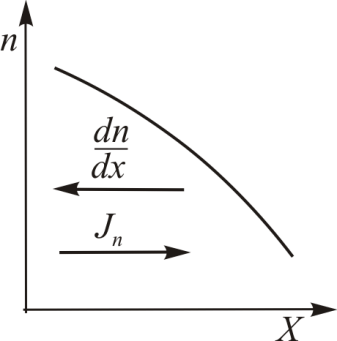где 
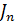- плотность потока концентрации «меченых» атомов, т.е. атомов, близких по размерам и свойствам атомам фона, например изотопов. 
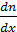– градиент концентрации меченых атомов, а 
– коэффициент самодиффузии. Размерности выше указанных величин таковы:
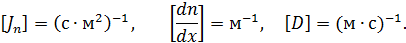
| Рис. 16.2. |
Дата добавления: 2015-08-11; просмотров: 1286;