Генерация подмножеств за счет их минимального изменения.

Кроме генерации подмножеств данного множества в лексикографическом порядке весьма интересны схемы генерации при которых каждое последующее подмножество отличается от предыдущего вставкой или удалением одного элемента. Первым, естественно, рассмотрим вопрос, связанный с существованием подобных схем. Для этого вначале разберем частные генерации в зависимости от мощности базового множества, затем обобщим их. Считаем, что конкретные подмножества представлены в виде характеристических векторов.

Пусть n - мощность базового множества.

n = 1

1. (0); либо 1. (1);

2. (1). 2. (0).

n = 2

1. (0,0); либо ему симметричный 1. (0,0);

2. (1,0); 2. (0,1);

3. (1,1); 3. (1,1);

4. (0,1). 4. (1,0).

Других вариантов, начинающихся с пустого множества, нет!

n =3

1. (0,0,0,)

2. (1,0,0)

3. (1,1,0)

4. (0,1,0)

5. (0,1,1)

6. (1,1,1)

7. (1,0,1)

8. (0,0,1)

Упражнение. Построить другие варианты генерации подмножеств для n=3,начинающиеся с представления пустого множества.

Обобщим приведенные примеры:

Пусть C₁; C₂; ...; C_k-1; C_k содержит все k=2ⁿ двоичных представлений подмножеств множества из n элементов, причем каждое последующее подмножество отличается от предыдущего вставкой или удалением одного элемента. Тогда последовательность, генерирующая все подмножества множества из n+1 элемента может быть получена, например, так:

С₁0; C₂0; ...; C_K-10; C_K0; C_K1; C_K-11; ....;C₂1; C₁1.

Пример n=4

Так построенные последовательности двоичных слов являются симметрично отраженными относительно n-ой позиции.

Рассмотрим последовательность номеров изменяемых разрядов при переходе от одного двоичного слово к другому. Обозначим ее P_n. Тогда эта последовательность удовлетворяет следующему рекурсивному определению

P₁ = 1; P_n = P_n-1, n, P 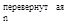, n>1.

По индукции легко доказать, что для n>0 P_n = P .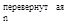

Таким образом последовательность P_n совпадает с ранее определенной последовательностью I_n.

Пример. n = 4, P₄ = I₄ = 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1.

Заметим, что значение m, 1£m£n, первый раз встречается как 2^m-1-ый член P_n, затем повторяется через каждые 2^m-1 членов последовательности.

Учитывая сказанное, можно построить на языке Паскаль следующий рекурсивный алгоритм:

program SET2 (,output);

const n= ;

var s : array [1..n] of 0..1;

i : integer;

procedure GRAY (m : integer);

begin