Program gen (input, output);

const n= ; n1= ; {n1=n+1}

var p:array [0..n1] of 1..n1;

{p[1],...,p[n] - генерируемая перестановка}

r:array [1..n] of 1..n;

{r - перестановка, обратная к p[1],...,p[n] }

d:array [1..n] of -1..1; {d - вектор направлений}

i,j,k,t: integer;

begin

for i:=1 to n do

for j:= 1 to n do write (p[j]); writeln;

i:=n;

while p[ r[i]+d[i] ] > i do

begin

{*} d[i]:=-d[i]; i:=i-1 {поиск перемещаемого элемента}

end;

k:=r[i]; t:=k+d[i];

j:=p[t]; p[k]:=j; p[t]:=i; {транспозиция элементов}

r[i]:=r[j]; r[j]:=k {корректировка обратной перестановки}

end

end.

Упражнения. 1. Доказать, что условием окончания генерирования всех перестановок является то, что перемещаемым становиться элемент 1.

2. Показать, что операторы строки {*} выполняются 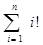раз. Определить временную вычислительную сложность алгоритма. Какова его емкостная вычислительная сложность?

3. Написать программу, которая генерирует перестановки с помощью одной транспозиции соседних элементов и при n=4 выдает следующую последовательность:

1. <1 2 3 4> 7. <3 1 2 4> 13. <4 3 2 1> 19. <4 2 1 3>

2. <2 1 3 4> 8. <1 3 2 4> 14. <4 3 1 2> 20. <4 2 3 1>

3. <2 3 1 4> 9. <1 3 4 2> 15. <4 1 3 2> 21. <2 4 3 1>

4. <2 3 4 1> 10. <3 1 4 2> 16. <1 4 3 2> 22. <2 4 1 3>

5. <3 2 4 1> 11. <3 4 1 2> 17. <1 4 2 3> 23. <2 1 4 3>

6. <3 2 1 4> 12. <3 4 2 1> 18. <4 1 2 3> 24. <1 2 4 3>.

Кроме приведенных алгоритмов генерации перестановок, возможны алгоритмы, основанные на других характеристических свойствах упорядочивания. Например, перестановки могут быть упорядочены с учетом числа циклов или инверсий и т.п. такие алгоритмы достаточно специфичны и здесь не рассматриваются. Классы перестановок с фиксированным числом циклов или инверсий представляют большой интерес в перечислительной комбинаторике и при анализе алгоритмов.