LEC (1)
end.
Комментарий. Процедура INVERT служит для восстановления первоначальной перестановки (свойство Л1) после генерации всех перестановок данного обобщенного блока. Процедура LEC осуществляет либо печать перестановки (строка {1}), если все n позиций уже сформированы, либо ( по свойству Л2) генерирует перестановки n-k+1 порядка как последовательность n-k+1 блоков перестановок n-k порядка с возрастающим по значению элементом на k позиции.
Тест n=3
 {2} {2}
| k=1 | i=3 | {4} | k=2 | p=2 3 1 | ||
| {2} | k=2 | i=3 | {2} | k=2 | i=2 | ||
| {1} | k=3 | вывод<1 2 3> | {1} | k=3 | вывод<2 3 1> | ||
| {3} | k=2 | i=3 | p=1 3 2 | {3} | k=1 | i=2 | p=3 2 1 |
| {4} | k=2 | p=1 3 2 | {4} | k=1 | p=3 1 2 | ||
| {2} | k=2 | i=2 | {2} | k=1 | i=3 | ||
| {1} | k=3 | вывод<1 3 2 | {3} | k=2 | i=3 | ||
| {3} | k=1 | i=3 | p=2 3 1 | {1} | k=3 | i=3 | вывод<3 1 2> |
| {4} | k=1 | p=2 1 3 | {3} | k=2 | i=3 | p=3 2 1 | |
| {2} | k=1 | i=2 | {4} | p=3 2 1 | |||
| {2} | k=2 | i=3 | {2} | k=2 | i=2 | ||
| {1} | k=3 | вывод<2 1 3> | {3} | k=3 | вывод<3 2 1> | ||
| {3} | k=2 | i=3 | p=2 3 1 |
Упражнение. Проведите формальное доказательство правильности алгоритма процедуры LEC. Указание. Методом математической индукции докажите, что если p[k]<...<p[n], то вызов LEC(k) приводит к генерированию всех перестановок множества p[k],...,p[n] в лексикографическом порядке при неизменных значениях p[1],...,p[k-1].
Для оценки сложности приведенной рекурсивной программы наряду со средним числом количества транспозиций элементов перестановки, нам необходимо определить среднее число вызовов процедуры LEC, как функции от n - порядка перестановок.
Пусть Bn - число вызовов процедуры LEC при генерации всех перестановок n - порядка программой LEX1. Для Bn справедливо следующее рекуррентное соотношение
B1=1
Bn= n×Bn-1+1
Его решением является последовательность Bn=n!× 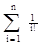 . Это приводит к тому, что в среднем на одну перестановку приходится e-1 вызовов процедуры LEC. Этот результат позволяет сравнить алгоритмы LEX и LEX1. Фактически сравнение сводится к оценке того, что эффективнее реализуется на конкретной ЭВМ: e-1 вызовов рекурсивной процедуры или 3.077 сравнений целых чисел.
. Это приводит к тому, что в среднем на одну перестановку приходится e-1 вызовов процедуры LEC. Этот результат позволяет сравнить алгоритмы LEX и LEX1. Фактически сравнение сводится к оценке того, что эффективнее реализуется на конкретной ЭВМ: e-1 вызовов рекурсивной процедуры или 3.077 сравнений целых чисел.
Наряду с лексикографическим порядком достаточно часто встречается генерирование перестановок в антилексикографическом порядке.
Определение. Пусть f=<a1,...,an>, g=<b1,...,bn>, будем говорить, что f<g в антилексикографическом порядке, если существует k£n такое, что ak>bk и aq=bq для q>k.
Пример. При n=4 в антилексикографическом порядке перестановки располагаются так:
| 1. <1, 2, 3, 4> | 7. <1, 2, 4, 3> | 13. <1, 3, 4, 2> | 19. <2, 3, 4, 1> |
| 2. <2, 1, 3, 4> | 8. <2, 1, 4, 3> | 14. <3, 1, 4, 2> | 20. <3, 2, 4, 1> |
| 3. <1, 3, 2, 4> | 9. <1, 4, 2, 3> | 15. <1, 4, 3, 2> | 21. <2, 4, 3, 1> |
| 4. <3, 1, 2, 4> | 10. <4, 1, 2, 3> | 16. <4, 1, 3, 2> | 22. <4, 2, 3, 1> |
| 5. <2, 3, 1, 4> | 11. <2, 4, 1, 3> | 17. <3, 4, 1, 2> | 23. <3, 4, 2, 1> |
| 6. <3, 2, 1, 4> | 12. <4, 2, 1, 3> | 18. <4, 3, 1, 2> | 24. <4, 3, 2 ,1> |
Упражнение.
1.Сформулируйте свойства А1-А3 антилексикографического порядка, аналогичные свойствам Л1-Л3 для лексикографического порядка.
2.Определите соотношения между некоторой перестановкой и непосредственно следующей за ней в антилексикографическом порядке.
3.Постройте нерекурсивный алгоритм ANTYLEX, порождающий все перестановки в антилексикографическом порядке (сравните с [1]).
4.Постройте рекурсивный алгоритм ANTYLEX1, порождающий все перестановки в антилексикографическом порядке.
Дата добавления: 2015-08-11; просмотров: 841;
