Генерация перестановок в лексикографическом порядке.
АЛГОРИТМЫ КОМБИНАТОРИКИ
(лекции 2001 фрагменты)
Санкт-Петербург
ТЕМА 2. ГЕНЕРАЦИЯ ПЕРЕСТАНОВОК
Генерация перестановок в лексикографическом порядке.
При решении некоторых задач возникает необходимость генерирования перестановок n-го порядка. Чаще всего генерирование перестановок связано с задачами перебора, в которых решение данной представляет собой некоторую перестановку, обладающую конкретным заданным свойством. Для поиска искомой перестановки мы перебираем все возможные перестановки и проверяем для каждой из них выполнение этого конкретного свойства. Последовательное генерирование перестановок определяет на множестве всех перестановок некоторый порядок, а именно: пусть f и g перестановки, тогда f<g, если в этой генерации перестановка f появляется раньше перестановки g.
Например, предположим, мы разобрали кубик Рубика на отдельные части и собрали его случайным образом. После этого мы хотим проверить, можно ли его преобразовать таким образом, чтобы все его грани были одного цвета. Моделирование подобной задачи на компьютере явно потребует генерации перестановок.
С другой стороны, при проектировании решения задачи обычно имеются вполне определенные аргументы в пользу выбора той или иной упорядоченности перестановок при генерации. Фактически эта упорядоченность определяет алгоритм генерации перестановок. Чаще всего эти алгоритмы строятся по схеме, когда каждая последующая перестановка вычисляется как некоторая функция от предыдущей.
Замечание. Интересен вопрос, какого порядка перестановки можно генерировать, в разумное время, на современных ЭВМ? Вследствие того, что общее число перестановок n-го порядка равно n!, современные ЭВМ позволяют генерировать перестановки не более чем 16-го порядка (обоснуйте это!).
Вначале мы рассмотрим алгоритмы генерации всех перестановок в лексикографическом порядке. Этот порядок свойственен расположению слов в различных словарях, поэтому его часто называют словарным. Он характеризуется тем, что буквы алфавита считаются упорядоченным множеством, а слова в словаре располагаются вначале с меньших (ранее перечисленных в алфавите) букв, а затем с больших. Слова, начинающиеся с одинаковых букв, располагаются в зависимости от упорядоченности вторых букв в слове, и так далее. Для перестановок множества {1,2,…,n} числа считаются упорядоченными естественным образом. Формально можно дать следующее определение лексикографического порядка для перестановок.
Определение. Пусть f=<a1,...,an>, g=<b1,...,bn>, будем говорить, что f<g в лексикографическом порядке, если существует k³1 такое, что ak<bk и aq=bq для q<k.
Пример. При n=4 в лексикографическом порядке перестановки располагаются так:
| 1. <1, 2, 3, 4> | 7. <2, 1, 3, 4> | 13. <3, 1, 2, 4> | 19. <4, 1, 2, 3> |
| 2. <1, 2, 4, 3> | 8. <2, 1, 4, 3> | 14. <3, 1, 4, 2> | 20. <4, 1, 3, 2> |
| 3. <1, 3, 2, 4> | 9. <2, 3, 1, 4> | 15. <3, 2, 1, 4> | 21. <4, 2, 1, 3> |
| 4. <1, 3, 4, 2> | 10. <2, 3, 2, 4> | 16. <3, 2, 4, 1> | 22. <4, 2, 3, 1> |
| 5. <1, 4, 2, 3> | 11. <2, 4, 1, 3> | 17. <3, 4, 1, 2> | 23. <4, 3, 1, 2> |
| 6. <1, 4, 3, 2> | 12. <2, 4, 3, 1> | 18. <3, 4, 2, 1> | 24. <4, 3, 2, 1> |
Лексикографический порядок может быть интерпретирован так. Пусть каждая перестановка интерпретируется как целое число, записанное в n-ричной позиционной системе (с цифрами ‘0’«’1’,...,’n-1’«’n’). Тогда генерация их в лексикографическом порядке - это перечисление в порядке возрастания чисел, состоящих из n разных цифр.
Наша цель заключается в построении алгоритма генерации всех перестановок в лексикографическом порядке для произвольного n. Для этого мы выясним, как должна выглядеть следующая перестановка в генерации, если мы знаем текущую, при условии, что текущая перестановка не является последней в генерации. Рассмотрим подробнее свойства лексикографического порядка генерации перестановок:
Л1) В первой перестановке элементы располагаются в возрастающей последовательности, в последней - в убывающей (докажите это свойство для произвольного n).
Л2) Последовательность всех перестановок можно разбить на n блоков длины (n-1)!, соответствующих возрастающим значениям элемента в первой позиции. Остальные n-1 позиций блока, содержащего элемент p в первой позиции, определяют последовательность перестановок множества {1,...,n}/{р} в лексикографическом порядке.
Это свойство легко иллюстрируется приведенным примером генерации перестановок 4-порядка. Нетрудно видеть, что все перестановки 4-порядка разбиты на четыре столбца, при этом у перестановок первого столбца на 1-ой позиции расположен элемент 1, у второго - элемент 2 и так далее. Кроме того, в каждом столбце элементы, расположенные в перестановках со 2-ой по 4-ую позиции, образуют перестановки этих элементов в лексикографическом порядке. Для первого столбца перестановки элементов 2,3,4; для второго - 1,3,4; третьего - 1,2,4; для четвертого 1,2,3. Отметим также, что в каждом столбце элементы, расположенные со 2-ой по 4-ую позиции в первой перестановке, образуют возрастающую последовательность, а в последней перестановке эти же элементы расположены в убывающей последовательности (свойство Л1 лексикографического порядка).
Таким образом, если мы рассмотрим перестановки каждого столбца, то для элементов, расположенных со 2-ой по 4-у позиции, полностью выполняются свойства Л1 и Л2. Это замечание приводит к следующему обобщению свойства Л2 для перестановок произвольного порядка:
Л3) Последовательность всех перестановок можно разбить на n*(n-1)*...*(n-k+1) блоков выбором значений р1,...,pk элементов, расположенных на первых k позициях. При этом блок p1,...,pk предшествует блоку q1,...,qk, если р1,...,pk меньше q1,...,qk в лексикографическом порядке. Кроме того, для перестановок каждого такого обобщенного блока элементы, расположенные с k+1-ой по n-ую позиции, представляют собой генерацию перестановок этих элементов в лексикографическом порядке.
Теперь мы готовы сформулировать самое важное свойство лексикографического порядка, на основе которого легко преобразовать текущую перестановку в следующую. Это свойство можно записать так:
Л4) Любая текущая перестановка является заключительной для некоторого обобщенного блока. Этот блок определяется элементами текущей перестановки, расположенными на позициях в конце перестановки и представляющими собой максимально возможную убывающую последовательность значений элементов перестановки. Справедливость последнего замечания следует из свойства Л1 лексикографического порядка.
В дальнейшем максимально возможную убывающую последовательность значений элементов перестановки, расположенную на позициях в конце перестановки, будем называть “хвостом” перестановки.
Примеры. Рассмотрим приведенную выше генерацию перестановок 4-го порядка, тогда:
Перестановка <2,1,4,3> является заключительной для блока, состоящего из перестановок 7.<2,1,3,4> и 8.<2,1,4,3>, элементы 4,3 образуют ее хвост;
Перестановка <3,1,2,4> является заключительной для блока, состоящего из одной перестановки 13.<3,1,2,4>, ее хвост состоит из одного элемента - 4;
Перестановка <2,4,3,1> является заключительной для второго столбца приведенной генерации, ее хвост - 4,3,1;
Перестановка <4,3,2,1> является заключительной для всей генерации перестановок 4-го порядка, ее хвост совпадает со всей перестановкой.
Как же воспользоваться этим свойством, чтобы преобразовать текущую перестановку в следующую. Это можно сделать по следующему алгоритму:
1. Выделяем хвост текущей перестановки;
2. Если он не совпадает со всей перестановкой, то ищем в хвосте первый с конца перестановки элемент, больший элемента перестановки, расположенного непосредственно перед ее хвостом (если перестановка совпадает со своим хвостом, то она является заключительной во всей генерации);
3. Меняем местами элемент, найденный в предыдущем пункте, с элементом, расположенным непосредственно перед хвостом перестановки;
4. Располагаем все элементы, преобразованного в пункте 3 хвоста перестановки, в обратном порядке (инвертирование преобразованного хвоста перестановки).
Примеры. Перестановка <2,1,4,3> преобразуется по вышеприведенному алгоритму в перестановку <2,3,1,4>, а перестановка <3,1,2,4> в <3,1,4,2>. Рассмотрим перестановку 15-порядка <15,2,4,3,1,13,7,10,14,12,11,9,8,6,5>, она преобразуется в перестановку <15,2,4,3,1,13,7,11,5,6,8,9,10,12,14>.
Упражнение. В какие перестановки преобразуются следующие перестановки: а) n=3, <2,3,1>; б) n=5, <2,5,4,3,1>;
в) n=7, <4,5,2,3,1,6,7>; г) n=8, <2,4,3,6,8,7,5,1>.
Замечание 1. Можно провести формальное доказательство того факта, что преобразованная по данному алгоритму перестановка действительно совпадает со следующей после текущей перестановки в лексикографическом порядке. Однако мы такое доказательство опустим.
Замечание 2. Приведенный выше алгоритм преобразования текущей перестановки в следующую формально можно записать так:
Пусть p=<p1,...,pk,...,pj,...,pn>,где
1£k<n pk<pk+1 и для q:k<q<n следует pq>pq+1
(если p=<n,n-1,...,1>, то k=0),
j>k и pj>pk и для q:j<q£n следует pq<pk;
тогда следующая за p перестановка, при k¹0, имеет вид
<p1,...,pk-1,pj,pn,pn-1,...,pj+1,pk,pj-1,...,pk+1>.
Теперь мы легко можем написать на языке Паскаль алгоритм генерации всех перестановок в лексикографическом порядке. Он основан на поиске k и j в текущей перестановке, транспозиции элементов pk и pj, и инвертировании ее‘хвоста’:
program LEX;
const n=...; {порядок перестановок}
var р : array [0..n] of 0..n; { текущая перестановка}
k : 0..n; j,r,m : 1..n;
Begin
for k:=0 to n do p[k]:=k; {задание начальной перестановки}
k:=1;
while k<> 0 do
Begin
for k:=1 to n do write(p[k]); writeln; {вывод перестановки}
k:=n-1; while p[k]>p[k+1] do k:=k-1; {поиcк k}
j:=n; while p[k]>p[j] do j:=j-1; {поиск j}
r:=p[k]; p[k]:=p[j]; p[j]:=r; {транспозиция рк и pj }
j:=n; m:= k+1;
while j>m do {инвертирование хвоста перестановки}
begin r:=p[j]; p[j]:=p[m]; p[m]:=r; j:=j-1; m:=m+1 end
End
End.
Комментарий. Нулевой элемент включен в массив р для того, чтобы обеспечить конец цикла {поиск k}после генерации последней перестановки.
Упражнение. Протестируйте приведенную выше программу при n=3.
Оценим временную вычислительную сложность приведенной программы. Обычно временная вычислительная сложность программ, представленных на языке высокого уровня, оценивается как порядок роста числа исполняемых операторов программы в зависимости от некоторого параметра исходных данных [3]. Однако, в алгоритмах генерации перестановок такой подход малоэффективен, так как в процессе работы любого алгоритма генерации всех перестановок порождается n!перестановок, т. е. временная вычислительная сложность всегда будет, по крайней мере, O(n!) - величина слишком быстро растущая. Любая ‘экономия’ в реализации будет сказываться только на коэффициенте пропорциональности при n!. Поэтому для того, чтобы удобнее было сравнивать различные алгоритмы генерации перестановок, обычно вводят другие критерии оценки вычислительной сложности. Здесь разумно ввести два критерия - количество транспозиций элементов перестановки, выполняемых в среднем при генерации одной перестановки, и аналогичное среднее числа сравнений элементов перестановки в операторах {поиск k} и {поиск j}.
Оценим их число. Пусть Tk - число транспозиций, выполняемых при вызове оператора LEC(n-k+1), т. е. Tk –число транспозиций, которые необходимо выполнить при генерации перестановок k-го порядка. Имеем
Tk=k*Tk-1+(k-1)*(1+ë(k-1)/2û )=
k*Tk-1+(k-1)*ë(k+1)/2û,где ëaû = ‘целой части числа a’.
Первое слагаемое определяет число транспозиций при вызовах оператора LEC(n-k), а второе - число транспозиций, выполняемых в операторах {3} и {4}. Заметим, что T1=0.
Для решения этого рекуррентного уравнения сделаем замену переменной. Пусть Sk=Tk+ë(k+1)/2û, тогда
S1=1, Sk=k*(Sk-1+dk-1),
где dk=0, если k нечетно, и dk=1, если k четно.
Решение этого рекуррентного соотношения легко получается по индукции:
Sk=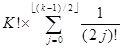 
,
т. е.
Tk=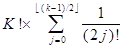 
- ë(k+1)/2û.
Учитывая, что 
»ch(1)»1.543 и ë(k+1)/2û=o(k!). получаем
Tk»k!*ch(1),
т. е. на генерирование одной перестановки в лексикографическом порядке требуется в среднем ch(1)»1.543 транспозиций.
Перейдем теперь к оценке числа сравнений элементов перестановки в операторах {поиск k}и {поиск j}; обозначим это число Сn.
Определим Сn как функцию от Сn-1. Отметим, что при генерации каждого из n блоков, определенных в Л2, требуется Cn-1 сравнений, а таких блоков n. Далее, при переходе от одного блока к другому оператор {поиск k} выполняется n-1 раз, а оператор {поиск J} при переходе от блока p к блоку p+1 (1£p<n) - p раз, т. е.
Cn= n*Cn-1+(n-1)*(n-1)+1+...+(n-1), C1=0
или
Cn= n*Cn-1+(n-1)*(3n-2)/2 C1=0.
Пусть Dn=Cn+(3n+1)/2, тогда D1=2, Dn=n*Dn-1+3/2,
и по индукции получаем
Dn=n!*(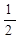 
+ 
)
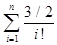или
учитывая, что е=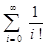 
,получаем Dn»n!*( 
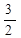e-1).
Тогда, Cn» n!*( 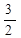e-1)-(3n+1)/2, учитывая, что (3n+1)/2=о(n!),получаем
Cn/n!»( 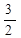e-1)
Таким образом, на генерирование одной перестановки алгоритмом LEX в среднем выполняется ( 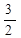e-1)» 3.077 сравнений.
Замечание. Применение методов рекурсивного программирования не требует выяснения того факта, как выглядит следующая перестановка после текущей в лексикографическом порядке. Легко построить соответствующую рекурсивную программу непосредственно на основе свойств Л1-Л3. Эта рекурсивная программа может быть написана так:
program LEX1 (output);
const n=...; {n порядок перестановок}
var p : array [1..n] of 1..n;
i,r : 1..n;
procedure INVERT (m : integer); {инвертирование p[m]...p[n] }
var i,j: 1..n;
begin i:=m; j:=n;
while i<j do begin r:=p[i]; p[i]:=p[j]; p[j]:=r;
i:=i+1; j:=j-1
end
end {INVERT};
procedure Lec (k:integer);
var i : 1..n;
begin
if k=n then
{1} begin for i:=1 to n do write (p[i]); writeln end
Else
for i:=n downto k do
{2} begin
LEC (k+1);
if i>k then
Begin
r:=p[i]; p[i]:=p[k]; p[k]:=r;
{3} INVERT (k+1)
{4} end
End
end {LEC};
Begin
for i:=1 to n do p[i]:=i;
Дата добавления: 2015-08-11; просмотров: 4054;