Циркуляция вектора индукции магнитного поля по замкнутому контуру. Вихревой характер магнитного поля

В электростатическом поле циркуляция вектора 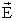по замкнутому контуру равна нулю.

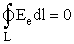
Найдем циркуляцию вектора 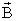по замкнутому контуру в магнитном поле. Рассмотрим магнитное поле прямого тока (рис. 16). Ток уходит за чертеж. Линии индукции охватывают контур, их направление связано с направлением тока правилом правого винта (буравчика).

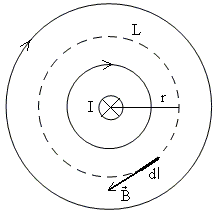
Рис. 16

Выберем мысленно замкнутый контур в форме окружности радиуса r. На рисунке 16 он изображен штриховой линией. Вычислим циркуляцию вектора 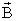по выбранному контуру. Значение индукции магнитного поля прямого тока на расстоянии r от него задается уравнением (9): 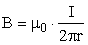. Выражение для циркуляции вектора 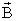по контуру запишем в виде:

,

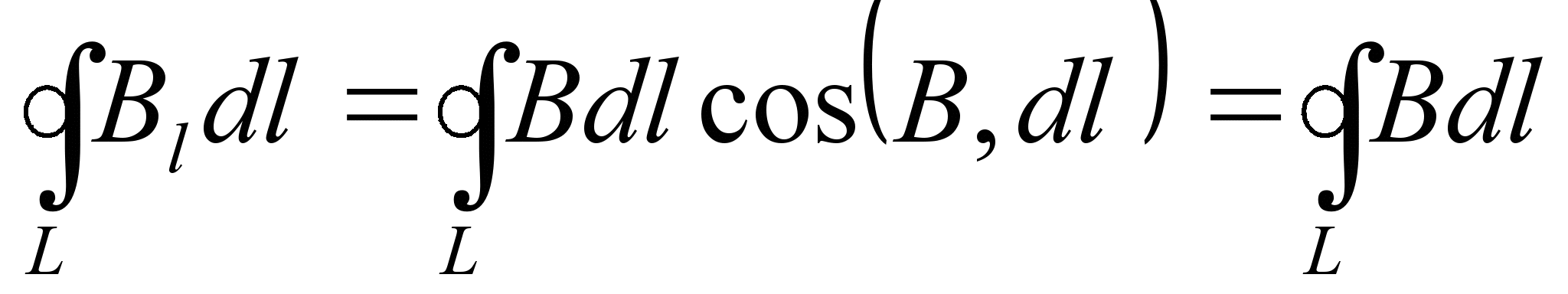так как вектор 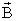в каждой точке линии магнитной индукции направлен по касательной, угол между элементом контура dl и 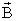равен нулю, тогда косинус угла между этими векторами равен единице.

Подстановка уравнения (9) приводит к выражению:

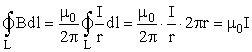
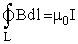
Циркуляция вектора 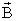по замкнутому контуру равна произведению магнитной постоянной μ₀ на ток, охватываемый контуром. Если контур охватывает несколько токов (рис. 17), то берется алгебраическая сумма токов.

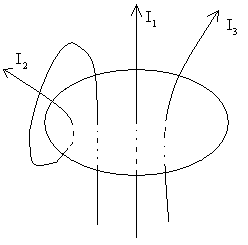
рис. 3.17

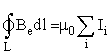
(13)

Это выражение носит название закона полного тока в вакууме. Для поля в веществе учитываются еще молекулярные токи.

Положительным считается ток, направление которого связано с направлением обхода контура правилом правого винта, ток противоположного направления считается отрицательным. Например для системы токов, изображенных на рис. 17

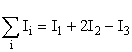
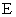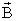Сравнивая выражения для циркуляции векторов и видим, что электростатическое и магнитное поля имеют принципиальное различие. Циркуляция вектора 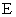всегда равна нулю, электростатическое поле потенциальное. Циркуляция вектора 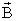не равна нулю, такое поле называется вихревым.

Теорема о циркуляции вектора 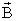имеет в учении о магнитном поле такое же значение, как теорема Остроградского-Гаусса в электростатике. Она позволяет находить магнитную индукцию поля, не применяя закон Био-Савара-Лапласа.
^