Применение закона Био-Савара-Лапласа к расчету поля прямого тока

Рассмотрим поле, созданное тонким прямым проводником с током бесконечной длины (рис. 13). Значение индукции магнитного поля 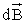в точке А, созданного элементом 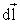тока I , определяется формулой (6) или в скалярном выражении – формулой (7).

Для того, чтобы определить индукцию магнитного поля 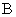, нужно сложить согласно (5) все элементарные векторы .

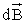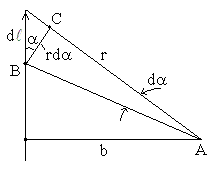
рис. 13

Все векторы 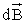в точке А имеют одинаковое направление (см. рис. 13), поэтому сложение векторов можно заменить сложением их модулей. Сделаем некоторые преобразования:

;

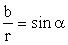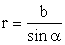
Учитывая, что угол dα , под которым виден участок проводника dl из точки А, мал, можно принять АВ ≈ АС; ВС = rdα, тогда

.

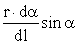
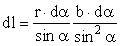Подставим полученные выражения для r и dl в формулу (7), а затем в (5).

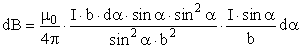
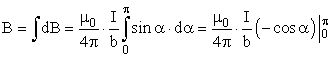
Угол α для всех элементов бесконечного прямого тока изменяется в пределах от 0 до π.В итоге:

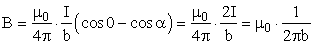
(8)

2. Расчет магнитного поля кругового тока

Поле в центре кругового тока.

По круговому контуру радиуса R течет ток I, требуется найти индукцию магнитного поля в центре контура, в точке О (рис. 14).

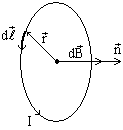
рис. 14

Рассмотрим элемент контура 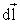с током I. Созданная им элементарная индукция будет равна: 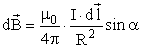, где α = π/2, значит sin π = 1. Направление векторов 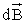от всех элементов 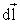кругового тока совпадает с направлением положительной нормали к контуру. После интегрирования получим:

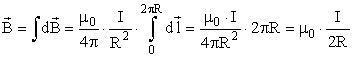
(9)