Графическое изображение магнитного поля. Поток вектора магнитной индукции

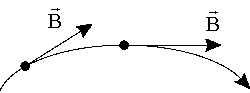
Рис. 6

Магнитное поле можно изобразить графически при помощи линий магнитной индукции. Линией магнитной индукции называют линию, касательная к которой в каждой точке совпадает с направлением вектора индукции магнитного поля (рис. 6).

Исследования показали, что линии магнитной индукции являются замкнутыми линиями, охватывающими токи. Густота линий магнитной индукции пропорциональна величине вектора 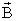в данном месте поля. В случае магнитного поля прямого тока линии магнитной индукции имеют форму концентрических окружностей, лежащих в плоскостях, перпендикулярных току, с центром на прямой с током. Направление линий магнитной индукции независимо от формы тока можно определить по правилу буравчика. В случае магнитного поля прямого тока буравчик необходимо вращать таким образом, чтобы его поступательное движение совпало с направлением тока в проводе, тогда вращательное движение ручки буравчика совпадет с направлением линий магнитной индукции (рис. 7).

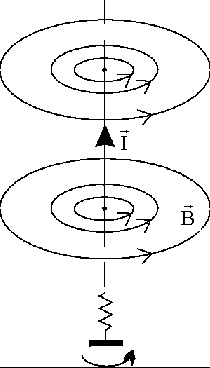
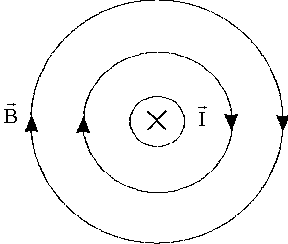
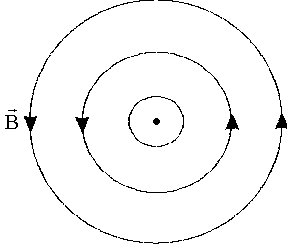
Рис. 7

На рис. 8 и 9 изображены картины линий магнитной индукции поля кругового тока и поля соленоида. Соленоид представляет собой совокупность круговых токов с общей осью.

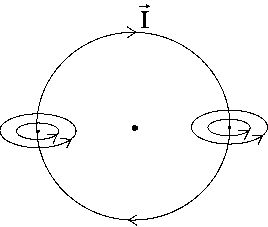
Рис. 8

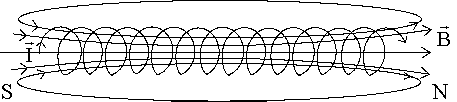
Рис. 9

Линии вектора индукции 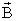внутри соленоида параллельны друг другу, густота линий одинакова, поле однородно ( 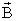= const). Поле соленоида аналогично полю постоянного магнита. Конец соленоида, из которого выходят линии индукции аналогичен северному полюсу – N, противоположный конец соленоида аналогичен южному полюсу – S.

Число линий магнитной индукции, пронизывающих определенную поверхность, называют магнитным потоком через эту поверхность. Обозначают магнитный поток буквой Ф_в (или Ф).

,

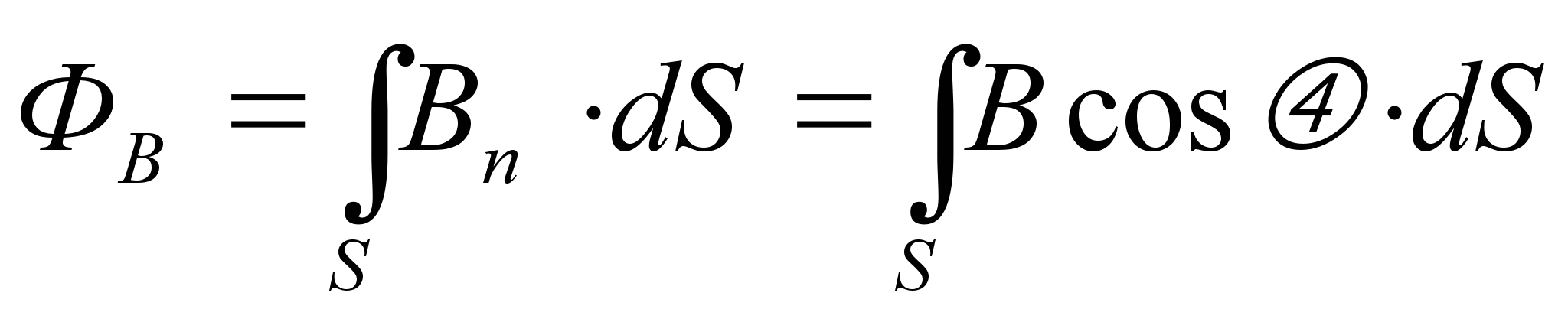(3)

где α – угол, образуемый вектором 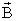и нормалью к поверхности (рис. 10).

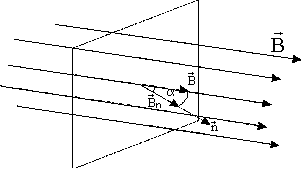
Рис. 10

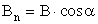– проекция вектора 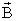на нормаль к площадке S.

Измеряется магнитный поток в веберах (Вб): [Ф]=[B]× [S]=Тл× м² = =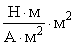

.

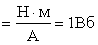Рис. 11

Если вычисляется магнитный поток, пронизывающий контур, состоящий не из одного витка, а из нескольких витков, то вводится потокосцепление Ψ (рис. 11).