Распределения Максвелла и Больцмана. Явления переноса

План лекции:

1. Закон Максвелла о распределении молекул по скоростям. Характерные скорости молекул.

2. Распределение Больцмана.

3. Средняя длина свободного пробега молекул.

4. Явления переноса:

а).диффузия;

б).внутреннее трение (вязкость);

в).теплопроводность.

1. Закон Максвелла о распределении молекул по скоростям. Характерные скорости молекул.

Молекулы газа движутся хаотически и в результате столкновений скорости их меняются по величине и направлению; в газе имеются молекулы как с очень большими, так и с очень малыми скоростями. Можно поставить вопрос о числе молекул, скорости которых лежат в интервале от и для газа в состоянии термодинамического равновесия в отсутствии внешних силовых полей. В этом случае устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям , которое подчиняется статистическому закону , теоретически выведенному Максвеллом.

Чем больше общее число молекул N, тем большее число молекул DN будет обладать скоростями в интервале оти ;чем больше интервал скоростей 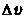, тем у большего числа молекул 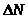значение скоростей будет лежать в указанном интервале.

~

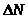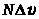
Введем коэффициент пропорциональности f(u).

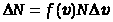, (1)

где f(u) называется функцией распределения, которая зависит от скорости молекул и характеризует распределение молекул по скоростям.

Если вид функции 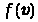известен, можно найти число молекул 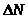, скорости которых лежат в интервале от до .

С помощью методов теории вероятности и законов статистики Максвелл в 1860г. теоретически получил формулу, определяющую число молекул 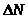, обладающих скоростями в интервале от до .

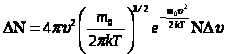, (2)

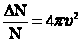
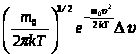- распределение Максвелла показывает, какая доля 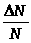общего числа молекул данного газа обладает скоростями в интервале от до .

Из уравнений (1) и (2) следует вид функции :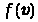

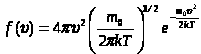- (3)

функция распределения молекул идеального газа по скоростям.

Из (3) видно, что конкретный вид функции 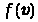зависит от рода газа (от массы молекулы m₀) и температуры.

Наиболее часто закон распределения молекул по 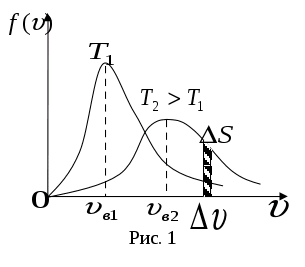скоростям записывают в виде:

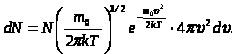
График функции 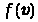асимметричен (рис. 1). Положение максимума характеризует наиболее часто встречающуюся скорость, которая называется наиболее вероятной. Скорости, превышающие u_в, встречаются чаще, чем меньшие скорости.

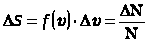- доля общего числа молекул, обладающих скоростями в этом интервале.

S_общ.= 1.

С повышением температуры максимум распределения сдвигается в сторону больших скоростей, а кривая становится более пологой, однако площадь под кривой не изменяется, т.к. S_общ.= 1.

Наиболее вероятной называют скорость, близкой к которой оказываются скорости большинства молекул данного газа.

Для её определения исследуем 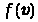на максимум.

, 4 ,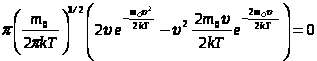

, .

, .

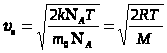Ранее было показано, что

, ,

=> .

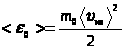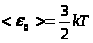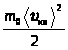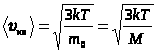В МКТ используют также понятие средней арифметической скорости поступательного движения молекул идеального газа.

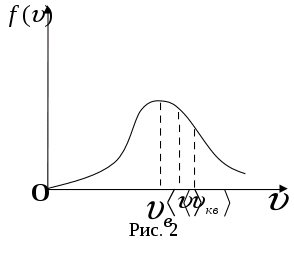
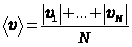- равна отношению суммы модулей скоростей всех молекул к

числу молекул.

.

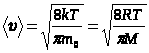Из сравнения видно (рис.2), что наименьшей является u_в.

2. Распределение Больцмана.

Два фактора - тепловое движение молекул и наличие поле тяготения Земли приводят газ в состояние, при котором его концентрация и давление убывают с высотой.

Если бы не было теплового движения молекул атмосферного воздуха, то все они сосредоточились бы у поверхности Земли. Если бы не было тяготения, то частицы атмосферы рассеялись бы по всей Вселенной. Найдем закон изменения давления с высотой.

Давление столба газа определяется формулой .

Поскольку с увеличением высоты давление уменьшается,

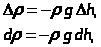
где r плотность газа на высоте h.

Найдем p из уравнения Менделеева- Клапейрона

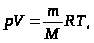
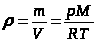
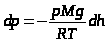или .

Проведем расчет для изотермической атмосферы, считая, что Т=const (не зависит от высоты).

.

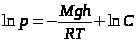при h=0 , , ,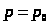

, , ,

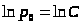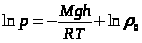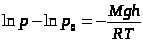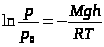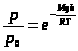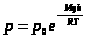- барометрическая формула, определяет давление газа на любой высоте.

Получим выражение для концентрации молекул на любой высоте.

,

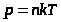
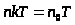
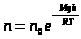
Т. к. 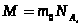, а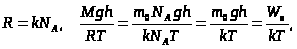

где 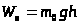- потенциальная энергия молекулы на высоте h.

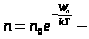распределение Больцмана во внешнем потенциальном поле.

Следовательно, распределение молекул по высоте есть их распределение по энергиям. Больцман доказал, что это распределение справедливо не только в случае потенциального поля сил земного тяготения, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.

Из распределения Больцмана следует, что молекулы располагаются с большей концентрацией там, где их потенциальная энергия меньше.

Распределение Больцмана - распределение частиц в потенциальном силовом поле.

3. Средняя длина свободного пробега молекул.

Вследствие хаотического теплового движения молекулы газа непрерывно сталкиваются друг с другом, проходят сложный зигзагообразный путь. Между 2-мя столкновениями молекулы движутся равномерно прямолинейно.

М 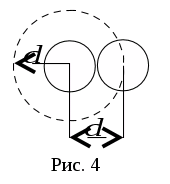инимальное расстояние, на которое сближаются центры 2-х молекул при соударении, называется эффективным диаметром молекулы d (рис. 4).

Величина 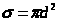называется эффективным сечением молекулы.

Найдем среднее число столкновений молекулы однородного газа в единицу времени. Столкновение произойдёт, если центры молекул сблизятся на расстояние, меньшее или равное d. Предполагаем, что молекула движется со скоростью 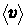, а остальные молекулы покоятся. Тогда число столкновений определяется числом молекул, центры которых находятся в объёме, представляющем собой цилиндр с основанием 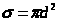и высотой, равной пути, пройденном молекулой за 1с, т.е. .

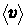В действительности все молекулы движутся, и возможность столкновения 2-х молекул определяет их относительная скорость. Можно показать, что если для скоростей молекул принято распределение Максвелла, .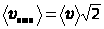

.

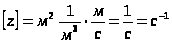Для большинства газов при нормальных условиях

.

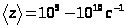Средняя длина свободного пробега - это среднее расстояние, которое проходит молекула между двумя последовательными соударениями. Оно равно отношению пройденного за время Dt пути к числу соударений за это время:

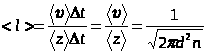
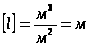
Для большинства газов при нормальных условиях .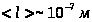

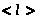обратно пропорциональна концентрации молекул.

Поскольку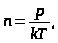

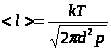
При T =const 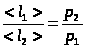, 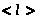обратно пропорциональна давлению.