Основы квантовой механики. Уравнение Шредингера

Вся совокупность сведений о свойствах света заставляет признать, что свет обладает одновременно и корпускулярными и волновыми свойствами, причем в одних явлениях (фотоэффект,

тепловое излучение, люминесценция) в большей степени проявляются корпускулярные свойства света, в других (интерференция, дифракция, дисперсия, поляризация) - волновые. Явно проявляется закономерность: чем короче длина волны, тем ярче проявляются квантовые (корпускулярные) свойства; чем больше длина волны, тем ярче проявляются волновые свойства света.

Вывод: противоречивые корпускулярные и волновые свойства даны в их неразрывном единстве, в органической слитности и представляют диалектическое единство. В синтезе волновых и корпускулярных свойств света мы видим, что в каждом явлении природы проявляются противоположности и что вместе с тем существует их диалектическое единство.

Выражением корпускулярно-волнового дуализма, лежащего в основе, существе самой природы света - двойственности его свойств, является существование прямой связи между корпускулярными и волновыми характеристиками света:

Е = h v, но Е = тс^г, тс² = hv;

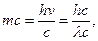
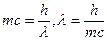, (4.9)

В 1924 г корпускулярно-волновой параллелизм оптики французский физик Луи де Бройль распространил на электроны, атомы и молекулы, сопоставив с движением каждой частицы некоторую волну, характеризующую ее волновые свойства. Между этой длиной волны и импульсом частиц mv де Бройль установил соотношение, аналогичное формуле (4.9):

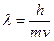(4.10)

Это соотношение получило название формулы де Бройля.

В 1927 году это было подтверждено экспериментально в опытах американских физиков Девиссона и Джермера по дифракции электронов. Позднее в опытах П.О.Тартаковского (Ленинград), Томсона, Вирля, Штерна и Джонсона на атомах гелия, водорода.

В 1925-1926 гг., еще раньше, чем идеи де Бройля были подтверждены экспериментально, представление о волновых свойствах частиц вещества было положено Шредингером, Гейзенбергом и Дираком в основу созданной ими квантовой механики.

По современным воззрениям квантовой объект - это не частица и не волна, и даже не то и не другое одновременно. Квантовый объект -это нечто третье, не равное простой сумме свойств волны и частицы, для выражения, которого у нас нет соответствующих понятий, соответствующего языка. Но поскольку сведения о микрообъекте, о его характеристиках мы получаем в результате взаимодействия его с классическим прибором (макрообъектом), то и описывать этот микрообъект следует в классических понятиях, т.е. использовать понятие волны и частицы. Мы вынуждены говорить на классическом языке, потому что другого у нас нет. Но для возможно более полного представления о микрообъекте мы должны использовать два типа приборов: один из них позволяет изучать волновые свойства микрообъекта, другой - его корпускулярные свойства. Эти свойства являются несовместимыми в отношении их одновременного проявления, но они оба в равной мере характеризуют микрообъект, а потому не противоречат, а дополняют друг друга. Эта идея и была высказана Н. Бором и положена им в основу важнейшего методологического принципа современной науки - принципа дополнительности.

Принцип дополнительности, как общий принцип познания, может быть сформулирован так: всякое истинно глубокое явление природы не может быть определено однозначно с помощью слов нашего языка и требует для своего определения, по крайней мере, двух взаимоисключающих, дополнительных понятий. К числу таких явлений относятся квантовые явления, жизнь и др.

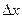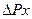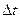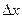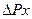
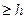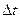
С принципом дополнительности связано и так называемое «соотношение неопределенностей», сформулированное в 1927 т. В. Гейзенбергом. Он показал, что эти неопределнности (неточности) в значениях координаты ( ) и импульса ( ), энергии ( ) и времени ( ) удовлетворяют следующим соотношениям: · , · 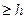. Эти соотношения утверждают, что (в отличие от классической физики) никогда нельзя одновременно точно знать оба параметра -координату и скорость, энергию и время. Оно указывает границу применимости классического описания к движению микрочастиц.

Итак, в противоположность классической механике в квантовой механике мы не можем точно указать, по какой траектории будет двигаться электрон. Мы можем только вычислить вероятность нахождения электрона в определенном месте пространства в данный момент времени. Амплитуда электронной волны 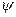также волновая

функция, зависит от координат и в общем случае - от t. Тогда амплитудное уравнение электронной волны, длина волны которой определяется по формуле де Бройля запишется:

+ + +

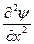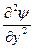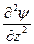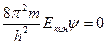
Это уравнение справедливо для свободного электрона, на который никакие силы не действуют. Если же электрон движется в некотором силовом поле, то нужно учесть его потенциальную энергию:

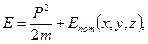
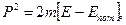
тогда

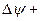
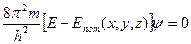(4.11)

и есть амплитудное уравнение Шредингера для стационарных состояний (не содержит времени). В частности, -оно может быть использовано при описании электрона в атоме на стационарной орбите. Чтобы волновая функция 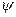являлась объективной характеристикой состояния микрочастиц, она должна удовлетворять ряду ограничительных условий, 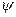— должна быть — конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть иной) и непрерывной (вероятность не может меняться скачком). Исследуя условия непрерывных, однозначных и конечных решений этого уравнения, получим ряд существенных выводов, в частности то, что условия квантования уже содержатся в данном уравнении и их не надо вводить (постулировать), как в теории Бора.

Таким образом, новая квантовая механика возвела в принцип двойственную (волновую и корпускулярную) природу физических тел. Гипотеза Бора оказалась одним из ее следствий.

Мы с Вами выяснили, что движение микрочастиц описывается уравнением Шредингера. Можно показать, что это уравнение имеет требуемые (т.е. однозначные, конечные и непрерывные) решения в следующих случаях: 1) При любых положительных значениях Е; 2) При дискретных отрицательных значениях энергии, равных:

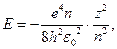где n=1,2,3, ...

Случай Е>0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся вновь на бесконечность. Случай Е<0 соответствует электрону, находящемуся в пределах атома.

Собственные функции 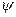уравнения содержат четыре целочис­ленных параметра, которые принято называть квантовыми числами. Введение квантовых чисел обусловлено тем, что электрон одновременно является и частицей, и волной, а потому его местоположение в атоме в точности указать принципиально невозможно. И хотя для наглядности введены орбиты электронов, на самом деле их нет. Мы можем говорить только о вероятности нахождения электрона в той или иной точке атомного объема. Часть пространства атома, где вероятность нахождения электрона максимальна, называется электронной орбиталью. (Термин «орбиталь» заменил слово «орбита» и во многом — слово «оболочка»). Таким образом, орбиталью считается замкнутая поверхность, внутри которой пребывание определенного электрона наиболее вероятно. Говорят, что внутри этой поверхности сосредоточена большая часть электронной плотности. Орбитали наружных электронов могут сливаться.

Энергия же, с которой электроны, находящиеся на орбитали, взаимодействуют с ядром атома, определяется точно, так как в данном случае электрон проявляет свойства частицы.

Строение электронной орбитали и ее энергия взаимодействия с ядром атома определяются атомными квантовыми числами, которые являются целочисленными параметрами собственных функций 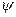уравнения Шредингера. Квантовые числа называются: главное, орбитальное, магнитное и спиновое.

Главное квантовое число п характеризует уровень энергии электрона и удаленность последнего от ядра атома. Сейчас известны следующие значения главных квантовых чисел и соответствующие им энергетические уровни атомов:

Главное квантовое число 1, 2, 3, 4, 5, 6, 7, 8.

Энергетический уровень К, L, M, N, О, Р, Q, R.

Энергия уровней возрастает с ростом главного квантового числа: наименьшим значением энергии обладает уровень К (п=1), ближайший к ядру атома.

Орбитальное квантовое число l определяет момент количества движения электрона относительно ядра атома. Значения l изменяются от 0 до (п -1). Как и главное квантовое число п, орбитальное

квантовое число тоже определяет энергию электрона, но уже в определенном энергетическом уровне. Следовательно, электроны с одинаковым п, но разным орбитальным квантовым числом, могут обладать различной энергией и занимать на одном и том же уровне различные энергетические подуровни. Однако разница энергии с n=1 и п=2 значительно больше, чем разница энергий подуровней с l=0 и l=1. В зависимости от величины l подуровни обозначаются такими буквами:

Значение l 0, 1, 2, 3,4.

Обозначение подуровня s, p, d, f, q.

Самым главным свойством орбитального квантового числа является то, что оно определяет форму электронной орбитали, которая обозначается так же, как и подуровни.

Энергия связи электрона в атоме с ростом радиуса энергетического уровня, на котором он находится, очень быстро уменьшается, наиболее связанные с ядром будут электроны с минимальным п. С ростом l энергия электрона тоже уменьшается. Например, 2s электрон связан с ядром атома крепче, чем 2р электрон.

Пока главное квантовое число мало, различия в энергии, вызванные изменением l, малы по сравнению с различиями, связанными с изменением п. Однако положение меняется, если п>3. Например, энергия орбитали 4s меньше энергии орбитали 3d.

Таким образом, квантовые числа n и l определяют энергию и форму электронных орбиталей. Магнитное квантовое число т_е определяет момент количества движения электрона относительно внешнего электромагнитного поля. Оно может принимать значения от l до - l или всего (2 l +1) значений. Количество магнитных квантовых чисел определяет число электронных орбиталей:

электронная орбиталь s, p, d, f, q;

величина/ 0, 1, 2, 3, 4;

количество т_е=(2 l +1) 1, 3, 5, 7, 9.

Расщепление энергетических уровней в магнитном поле обнаружено Зееманом, а в электрическом поле Штарком.

Магнитное спиновое квантовое число m_s. Спин характеризует собственный момент количества движения электрона вокруг своей оси. Существуют всего две независимые возможности такого вращения: против часовой стрелки и по часовой стрелке. Им отвечают два значения магнитного спинового квантового числа: m_s = +1/2 и m_s = -1/2. Расщепление соответствующих уровней подтверждено в опытах О.Штерна и В.Герлаха.

Значит, эти четыре квантовых числа п,l,m_s ,т_е, энергию и положение электрона в атоме.