Принцип неразличимости одинаковых частиц. Принцип Паули. Распределение электронов в многоэлектронных атомах

В разделе квантовой механики, рассматривающем свойства систем, состоящих из большого числа частиц таких как: сложный атом, электронный газ в металле, жидкий гелий, обнаруживший при низких температурах свойство сверхтекучести, прежде всего следует учитывать принцип неразличимости одинаковых частиц.

Если частицы, описываемые классической механикой, тождественны между собой, то это вовсе не означает их неразличимости. В самом деле, пусть нам известно их положение А, В, С в начальный момент времени (рис. 10). Мы можем пронумеровать частицы в этом состоянии. Если они перемещаются в пространстве и через некоторое время окажутся в точках А', В', C' то мы можем, несмотря на одинаковость частиц, точно определить, где находится каждая из ранее перенумерованных частиц. Такая возможность существует благодаря тому, что они движутся по определенным траекториям и, следя за этим движением, мы можем в любой момент времени отличить их друг от друга.

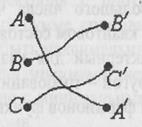
Рис. 10

В квантовой механике понятие траектории отсутствует. Это приводит к весьма глубоким изменениям при описании свойств системы многих микрочастиц. Если, например, электроны и перенумерованы в начальный момент времени, то в дальнейшем, если один из них окажется локализованным в какой-нибудь точке пространства, то номер его все равно принципиально не может быть определен. Так, при сближении двух атомов водорода становится достаточно большой вероятность пребывания в некоторой области пространства любого из электронов, принадлежащих вначале разным атомам. Предположим, что в результате эксперимента в какой-нибудь точке будет обнаружен электрон. Мы не можем, однако, при этом никаким способом определить какому из первоначально удаленных атомов водорода принадлежал он ранее.

Одинаковые микрочастицы принципиально неразличимы. Это ут­верждение и составляет содержание квантовомеханического принципа неразличимости одинаковых частиц. Принцип этот, не имеющий аналога в классической физике, проявляется в неизменности физических свойств системы при перестановке пары частиц. Волновая функция в этом случае может принять два значения: или 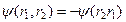. Функция системы, состоящей из двух частиц, при их перестановке или остается неизменной, или меняет знак на противоположный. Волновые функции, удовлетворяющие первому условию, называются симметричными, а удовлетворяющие второму условию антисимметричными.

Частицы, свойства которых описываются симметричными функциями (к ним относятся мезоны, фотоны, атомные ядра, состоящие из четного числа нуклонов и др.) называются частицами, подчиняющимися статистике Бозе-Эйнштейна, или бозонами. Антисимметричными функциями описываются частицы, подчиняющиеся статистике Ферма-Дирака (к ним относятся электроны, позитроны, протоны, нейтроны, нейтрино и др.).

В квантовой статистике, рассматривающей свойства систем, состоящих из очень большого числа частиц, определяется лишь среднее число в данном квантовом состоянии. При этом учитывается, с одной стороны, характерный для квантовой теории дискретный характер энергии, а с другой — требования принципа неразличимости одинаковых частиц. Для фермионов функция п имеет вид:

,

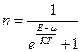а для бозонов

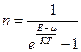
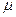В этих выражениях - химический потенциал системы, который представляет собой величину, численно равную изменению энергии в системе при добавлении к ней одной частицы. Если число частиц переменно, то 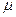= 0. Так, для фотонов, энергия которых равна Е=h 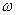получаем известное выражение Планка: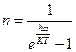

Распределение Ферми-Дирака и Бозе-Эйнштейна, как видно из выше­приведенных выражений, отличается лишь знаком перед единицей в знаменателе. Однако это приводит к очень большому различию в физических свойствах систем. Для Ферми частиц всегда n<1. Это ограничение составляет содержание принципа Паули, согласно которому в системе Ферми-частиц в одном и том же квантовом состоянии не может находиться более одной частицы. Это утверждение является следствием принципа неразличимости одинаковых частиц.

Известно, что химические и физические свойства атомов определяются расположением в них электронов или электронной конфигурацией. Заполнение энергетических уровней (оболочек) и электронных орбиталей (подуровней) происходит согласно трем законам.

Первый закон — принцип Паули (1924 г., швейцарский физик). В атоме не могут одновременно существовать электроны, характеризующиеся одинаковым значением всех четырех квантовых чисел.

Второй закон — правило Хунда. На одной электронной орбитали могут находиться два электрона с противоположными спинами. Общий спин атома, равный сумме спиновых квантовых чисел всех его электронов, стремится быть максимальным.

Третий закон - принцип минимума энергии. Электроны в атоме стремятся занять положение с минимальным значением энергии, т.е. как можно ближе к ядру атома.

Очень часто говорят «оболочка», «слой» электронов в атоме, что неверно. Мы же будем оперировать понятием «уровень», «подуровень», «орбиталь».

Принимая во внимание принцип Паули и учитывая 2 значения магнитного спинового квантового числа (т = ±1/2), принцип Паули можно сформулировать и следующим образом: в атоме не может быть больше 2-х электронов, движение которых характеризуется одинаковым значением 3-х квантовых чисел п, l, m .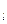

Поскольку магнитное квантовое число m 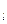принимает 2l+1 значений, то в сложных многоэлектронных атомах число электронов, характеризующихся одинаковыми значениями 2-х квантовых чисел п

и l не превышает 2(2l+1).

Максимальное число электронов на энергетическом уровне, характеризуемое значением одного квантового числа и, может быть подсчитано из условия, что l = n - 1 или 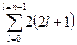. Эта сумма представляет сумму членов арифметической прогрессии, которая может быть вычислена по формуле: 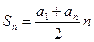, тогда 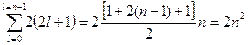, или представим таблицей:

Итак, на энергетическом уровне в общем виде может быть максималь­ное число электронов 2п². Тогда на каждом энергетическом уровне будет максимальное число электронов таким:

энергетический уровень К, L, M, N, О, Р, Q, R.

число электронов 2, 8, 18,32,50,72,98,128.

Причем, если атом обладает достаточно большим количеством электронов, то среди электронов, состояние движения которых характеризуется одинаковым квантовым числом п, не может существовать более (используя правило Хунда):

2-х S электронов (l=0), 10-ти d-электронов (l=2),

6-ти р электронов (l=1), 14-ти f-электронов (l=3), т.е. энергетический уровень может быть разбит на подуровни или орбитали.

Таким образом, каждому энергетическому уровню соответствует определенная конфигурация электронов, которая символически может быть записана так:

Уровень К, L, M, N,

Число электронов 2, 8, 18, 32,

Электронная конфигурация IS², 2S²2P⁶, 3S²3P⁶3d¹⁰,4S²4P⁶4d¹⁰4f¹⁴ ...

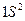
номер энергетического уровня число электронов на орбитале

или главное квантовое число

тип орбитали

Каждый заполненный энергетический уровень (оболочка) будет представлять энергетически устойчивую систему к химическим и оптическим взаимодействиям. Казалось бы, что повторения в структуре внешнего уровня говорит о повторении оптических и химических свойств атомов, однако, если посмотреть на периодическую систему элементов и сравнить с энергетическими уровнями (оболочками или слоями), то максимальное число электронов в периоде хотя и совпадает со значением максимального числа электронов на энергетическом уровне (слое), но повторения уровней (слоев) нет, как в периодической таблице Д.И.Менделеева.

I. Н₁,-Не₂ -2 IV.K 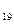-Kr₃₆ -18

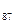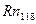II. Li₃-Ne₁₀ -8 V. Rb₃₇-Xe₅₄ -18 VII. Fr -Е -32

III.Na₁₁-Ar₁₈ -8 VI. Cs₅₅-Rn₈₆ -32

Это объясняется идеализацией условий построения (электрон находится в поле центральных сил и не учитывается взаимодействие электронов между собой). Если это учтем, то получим так называемые группы устойчивости, которые и определяют периодичность элементов.

Запишем эти группы:

I, II, III, IV, V, VI, VII
lS²,2S²2P⁶,3S²3P⁶,4S²3d¹⁰4P⁶,5S²4 5d¹⁰5P⁶,6S²4 f¹⁴5d¹⁰6P⁶, 7S²5f¹⁴6d¹⁰7P⁶

2, 8, 8, 18, 1.8, 32, 32.

Как видите, заполнение каждой группы устойчивости начинается с S подуровня (орбитали) и заканчивается застройкой Р подуровня (орбитали).

Таким образом, заполнение электронных орбиталей в атоме идет в последовательности lS2S2P3S3P4S3d4P5S4d5P6S4f5d6P7S5f6d7P. Заполнение d орбиталей происходит с запаздыванием на 1 период, а заполнение f орбиталей запаздывает на 2 периода.

Элемент, стоящий в конце периода (или группы устойчивости), не активный.

Атомы, обладающие минимальной энергией, называются невозбужденными атомами, или атомами в основном состоянии. Возбужденный атом —это атом, число электронов в котором равно заряду ядра атома, но они расположены на орбиталях с большей энергией, чем в невозбужденном атоме. Энергетический уровень элемента, который заполняется электронами, называется валентным. Валентность - свойство атома образовывать определенное число связей с другими атомами, в том числе и того же самого вещества.

Валентность химического элемента связана с отличием от нуля полного спина его электронной оболочки. Возможные значения валентности того или иного атома определяются допустимыми для него вариантами существования некомпенсированных электронных спинов. Рассмотрим несколько примеров. Атом водорода имеет один электрон в состоянии 1S и потому должен быть одновалентным. Гелий имеет два электрона в 1S состоянии. Спины этих электронов антипараллельны. Суммарный спин атома Не равен нулю, что и определяет химическую инертность гелия. Атом лития одновалентен. Его валентность обусловлена 28-электроном. Основное состояние атома бериллия характеризуется суммарным спином, равным нулю, но сравнительно слабое внешнее воздействие может перевести один из электронов 2S в 2р состояние. В результате образуется возбужденная конфигурация IS²2S2P и атом оказывается двухвалент­ным. Энергия, необходимая для образования такой возбужденной конфигурации, сообщается в процессе химической реакции. Атом бора одновалентен, но в результате одноэлектронного перехода 2S→2Р (при возбуждении) может стать трехвалентным.

После создания теории атома стала ясной причина периодичности свойств элементов, которая была открыта Д.И. Менделеевым в 1869 году. Если расписать число протонов и электронные конфигурации элементов, то можно увидеть, что с ростом заряда ядра электронная конфигурация валентного подуровня атома повторяется на новом энергетическом уровне. Так, для щелочных металлов строение валентного подуровня будет: у Li - 2S¹, yNa- 3S¹, у К-4 S¹y Rb- 5S¹, у Cs - 6S¹ и у Fr - 7S¹. Строение валентного подуровня у галогенов также повторяется: у F - 2S²2P⁵, у С1 - 3S²3P⁵, у Вr - 4S²4P⁵, у J - 5S²P⁵. Такая же повторяемость свойств имеет место у d элементов и/элементов.

Электронная конфигурация валентного уровня атомов периодически повторяется в зависимости от заряда ядра атома. Это и является главной причиной периодичности свойств элементов и их соединений. Основываясь на этом, современная формулировка периодического закона гласит: свойства элементов, а также форма и свойства соединений элементов находятся в периодической зависимости от величины заряда ядер их атомов и электронной конфигурации.

С положением элементов в периодической системе связаны особенности их спектров. Например, щелочные металлы имеют на внешней оболочке один электрон, переход которого на более высокие возбужденные уровни приводит к возникновению спектра с хорошо выраженными сериями. Такие спектры называются одноэлектронными. Двухэлектронные спектры возникают при возбуждении атомов, имеющих на внешней оболочке (уровне) два электрона. Структура таких спектров сложнее одноэлектронных. При возбуждении электронов, находящихся на внутренних уровнях (оболочках) атомов, возникают рентгеновские спектры. Характерной чертой рентгеновских спектров является их простота и единообразие, по сравнению с оптическими. Рентгеновские спектры всех элементов состоят из небольшого числа линий, сходным образом располо­женных относительно друг друга и имеющих одну и ту же тонкую структуру. При увеличении атомного номера весь рентгеновский спектр как бы смещается в область коротких длин волн, не меняя своей структуры. Простота и монотонный характер изменения рентгеновских спектров с изменением атомного номера указывает на то, что рентгеновские спектры связаны с возбуждением электронов, находящихся именно во внутренних уровнях оболочки атома.

Свое графическое изображение периодический закон Д. И. Менделеева нашел в виде периодической системы элементов. Име­ется несколько вариантов ее представления. Периодами называются горизонтальные ряды элементов, а группами - вертикальные.

Периодический закон Д. И. Менделеева подтвердил наиболее общие законы развития природы (единства и борьбы противоположностей, перехода количества в качество, отрицание отрицания) и явился ярким примером проявления закона перехода количества в качество и закона развития материи по спирали. Увеличение заряда ядра атома приводит к изменению его качественной химической природы. Это изменение носит спиралевидный периодический характер: от периода к периоду свойства элементов повторяются, но на новом витке спирали. Каждый период является новым, более широким витком этой спирали, на котором усиливаются свойства элементов предыдущего витка, выявляются новые черты их химического поведения.

Закон Д. И. Менделеева - живое воплощение диалектического материализма. Значение его в целом весьма велико. Периодический закон подтолкнул развитие учения о старении атома и лег в основу

работ Э. Резерфорда и Н. Бора. Используя периодический закон, геологи более целенаправленно стали искать месторождения, основываясь на подобии их свойств. Периодический закон позволяет предсказать способы обнаружения синтезируемых трансурановых элементов. Признанием значимости периодического закона и заслуг первооткрывателя - Д, И. Менделеева является присвоение 101-му элементу имени Менделеева.