Элементы механики жидкостей

Для описания движения идеальных жидкостей необходимо использовать теорему о неразрывности струи и уравнение Бернулли. Жидкость считается идеальной, если перемещение одних частей жидкости относительно других не вызывает сил трения, т.е. внутреннее трение (вязкость) отсутствует. Уравнение Бернулли для стационарно текущей трубки идеальной жидкости записывается:

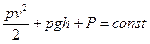(3.4)

где р - плотность несжимаемой жидкости; v - скорость в сечении выбранной трубки жидкости; h - высота трубки жидкости; Р -гидравлическое давление.

Уравнение достаточно хорошо выполняется и для реальных жидкостей, внутреннее трение в которых не очень велико. Уравнение Бернулли является одним из основных законов механики жидкостей и газов (гидро- и аэродинамики), имеющее большое прикладное значение. С учетом этого закона через специальные трубопроводы вода или газ поступает на лопасти рабочего колеса гидротурбины или газотурбины и приводит его во вращение. На основе уравнения Бернулли действуют: водоструйный насос, карбюратор двигателя внутреннего сгорания, пульверизатор, опрыскиватель растений, ингалятор и другие распылители жидкости. Не обходится без уравнения Бернулли и объяснение возникновения подъемной силы самолета.

Если молекулы отличаются одна от другой какой-либо характерной величиной (энергией, массой, импульсом и др.), причем их распределение по значениям указанной характеристики неоднородно, то вследствие теплового движения молекул эта. величина переносится из одного места в другое. В результате возникает поток рассматриваемой величины, обуславливающий ряд явлений, называемых явлениями переноса. К ним относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение или вязкость (обусловлено переносом импульса). Реальная жидкость, в отличие от идеальной, обладает вязкостью, обусловленной сцеплением между ее молекулами. Единицей вязкости в системе СИ является Паскаль-секунда и обозначается Па∙с. Вязкость жидкости во много раз превосходит вязкость газов. Вязкость жидкости находится в пределах ( 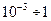) Па∙с и с повышением температуры уменьшается. 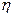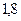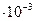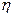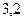Например у воды при 0°С = Па∙с, а при 90°С = 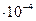Па∙с. Необходимо различать в движении жидкости два вида ее течения: ламинарное (параллельными слоями) и турбулентное (перемешивающееся, вихревое). Английский ученый Рейнольдc установил, что характер течения зависит от значения безразмерной величины 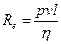, где p - плотность жидкости (газа); l- характерный для поперечного сечения потока размер. Величина R_e называется числом Рейнольдса. При малых значениях R_e ≤1000 - наблюдается ламинарное течение. При значении R_e ≥1000 течение приобретает турбулентный характер. Число Рейнольдса может служить критерием подобия для течения

жидкости в трубах, каналах и т.д. Характер течения различных жидкостей (газов) в трубах разных сечений будет совершенно одинаков, если каждому течению соответствует одно и то же значение R_e .

Благодаря вязкости тело, движущееся в жидкости, увлекает прилегающие к нему слои жидкости и потому испытывает сопротивление (трение) со стороны жидкости. Сила сопротивления зависит от скорости движения тела, его размеров и формы. Стокс установил, что при малых R_e или небольших скоростях движения тел шарообразной формы сила сопротивления жидкости пропорциональна вязкости жидкости 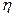, радиусу шара r и скорости движения v, таким образом:

F = 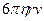, (3.5)

Закон Стокса (3.5) применим также к движению шарообразных тел в газе, например к случаю падения дождевых капель в атмосфере. Если движение тела происходит в турбулентном потоке, сила трения резко возрастает по сравнению с ее значением в ламинарном потоке и становится пропорциональной уже не первой степени, а квадрату и даже кубу скорости. Турбулентное движение можно, например, наблюдать в водном потоке на узких и мелких участках русла реки. Здесь появляются характерные водяные вихри-водовороты. В воздушном потоке это движение наблюдается, например, вблизи строений: возникающие при сильном ветре воздушные вихри поднимают с Земли и крутят пыль, обрывки бумаги и другие легкие предметы.

Знакомство с физическими величинами: скоростью, ускорением, силой, работой, мощностей энергией позволяет однозначно уяснить, что наиболее перспективными будут та техника и технология, которые обладают большей производительностью при одинаковой металлоемкости, энергоемкости, надежности и экологичности. Все эти понятия имеют не абстрактное, а самое существенное значение в экономике любого производства и не могут игнорироваться их руководством. Поскольку производительность труда находится в прямой зависимости от механизации и автоматизации процесса производства, то они являются основополагающими аргументами в развитии и совершенствовании производственных процессов и укреплении экономики производства.