Динамика вращательного движения твердого тела

До настоящего времени мы рассматривали поступательное движение материальной точки. Вращательное движение встречается в природе и технике не менее часто, чем поступательное. Если взять не материальную точку, а систему материальных точек — твердое тело, то любое движение может быть представлено как результат двух элементарных движений: поступательного и вращательного. Мы уже установили закономерности для поступательного движения, то же следует сделать и для вращательного движения. Тогда мы сможем описать любое движение твердого тела.

Не случайно для изучения закономерности вращательного движения мы берем не материальную точку, а систему материальных точек — твердое тело, т.к. целый ряд закономерностей вращательного движения зависит от формы тела.

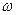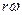При вращательном движении все частицы твердого тела описывают окружности вокруг оси вращения тела. Угловые скорость и ускорение для частиц тела одинаковы. Линейные скорость v и ускорение а пропорциональны расстоянию r частицы от оси вращения (v = , а = r ). Если тело может вращаться только вокруг неподвижной оси, то способность силы F вращать тело вокруг этой оси характеризует момент силы относительно оси М.

Момент силы относительно оси представляет собой осевой вектор, направленный по оси вращения, и определяется по правилу

правого буравчика. В общем случае записывается: М = 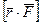, где 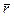- радиус-вектор, 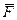- сила.

Вращающееся тело, как всякое движущееся тело, обладает кинетической энергией.

Сумма произведений масс элементарных частей тела на квадраты их расстояний до определенной оси называется моментом инерции относительно этой оси: 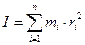. Для сплошного тела момент инерции выражается интегралом: 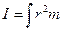. С учетом этого

кинетическая энергия вращающегося тела: .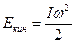

Величина момента инерции существует безотносительно к вращению. Каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси, подобно тому, как тело обладает массой, независимо от того, движется оно или покоится. Естественно предположить, что момент инерции зависит от формы тела и потому будет вычисляться по особой для каждой формы тела формуле.

Зависимость между моментом инерции тела и моментом силы, вызвавшим вращение тела, называется основным уравнением динамики вращательного движения и записывается: 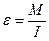. Это выражение можно записать и так: 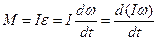. В последнем выражении 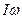— есть момент количества движения относительно оси вращения. Для замкнутой системы момент внешних сил М равен нулю, тогда - 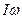= const. А эта запись выражает закон сохранения момента количества движения. Закон сохранения момента количества движения - фундаментальный закон природы. Хорошей демонстрацией этого закона служит скамья Жуковского, упражнения гимнастов, выполняющих сальто, взмахи рук и изменение положения тела человека на скользкой дороге (льду) для сохранения устойчивости положения и другие.