Колебания

Колебаниями называются любые движения, точно или приближенно повторяющиеся через одинаковые промежутки времени. Колебательные процессы широко распространены в природе и технике. Качание маятников часов, волны на воде, переменный электрический ток, свет, звук являются примерами колебаний различных физических величин, При движении маятника колеблется координата его центра тяжести. В случае переменного тока колеблются напряжение и ток в цепи. Эти два процесса качественно совершенно различны по своей физической природе. Однако количественные закономерности этих процессов имеют между собой очень много общего.

Колебания называются механическими, если они характеризуются изменением только механических величин (смещения, скорости, ускорения и т.п.) каких-либо тел или частей тела и могут происходить при наличии упругих сил, сил тяжести, а также других сил, например капиллярных.

Периодическими называются такие колебания, в которых каждое значение изменяющейся величины повторяется неограниченное числе раз через одинаковые промежутки времени. Наименьшее время, за которое повторяется каждое значение изменяющейся величины, называется периодом колебания и обозначается Т. Величина, обратная периоду колебания ( ), называется частотой периодических колебаний и обозначается буквой v. Единицей измерения частоты колебаний в системе СИ является герц-частота, при которой совершается одно колебание в секунду.

Простейшими являются гармонические колебания, т.е. такие колебания, при которых периодическое изменение величины (смещения) выражается косинусоидальным (или синусоидальным) законом:

х = Acos(ωt+φ₀), (3.6)

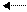где А — амплитуда колебаний — величина, равная наибольшему (по модулю) значению изменяющейся величины; (ωt+φ₀) - фаза гармонического колебания; φ₀ - начальная фаза, т.е. при t = 0; ω - угловая частота.

Динамика гармонических колебаний х = Acosωt позволяет для силы записать выражение:

F= 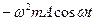(3.7)

Упростим запись формулы (3.7)

F= 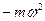х (3.8)

Если обозначить 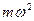через k, то получим для силы, вызывающей гар­монические колебания, формулу:

F= -kx, (3.9)

которая характеризует упругую силу. Поскольку движение под действием упругой силы является гармоническим колебанием, то найдем значение частоты и периода этих колебаний с учетом силы.

Исходя из вышеприведенного обозначения 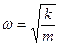, а следовательно частота гармонических колебаний:

(3.10)

Период колебаний:

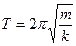(3.11)

В природе и технике наблюдаются гармонические колебания, воз­буждаемые действием не только упругих сил, а сил, величина которых каким-либо образом зависит от величины смещения колеблющейся точки. В этом случае условились силы, вызывающие гармонические колебания, но не являющиеся упругими, называть квазиупругими силами (по латыни guasi означает «как бы»).

Полная энергия колеблющегося тела определяется суммой кинетической и потенциальной энергий:

Е_к = и Е_п = . Зная, что х = Acos ωt, найдем v = 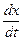— и получим выражение для полной энергии

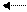
тела: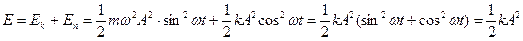

Полная энергия гармонического колебания пропорциональна квадрату амплитуды и коэффициенту упругости. В процессе движения происходит непрерывный переход кинетической энергии в потенциальную и обратно, но сумма их остается при этом постоянной. Когда точка проходит через положение равновесия х=0, потенциальная энергия обращается в нуль, а кинетическая максимальна и равна полной. Когда же колеблющаяся точка доходит до одного из своих крайних положений х =±A, то v = 0, кинетическая энергия превращается в нуль, а потенциальная - максимальна и равна полной.