Уравнение касательной и нормали к кривой.
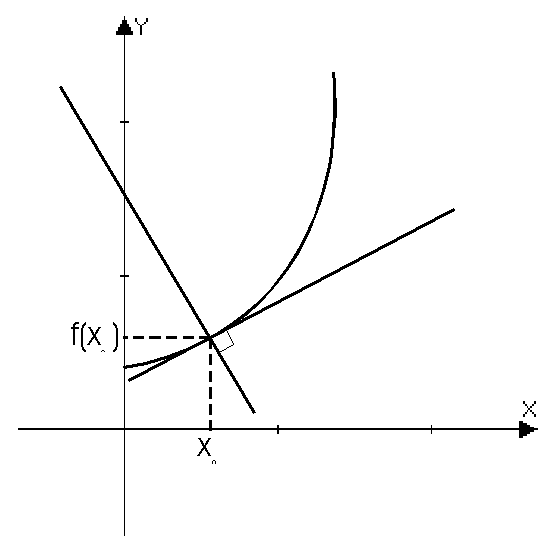 Из пучка прямых, проходящих через точку
Из пучка прямых, проходящих через точку 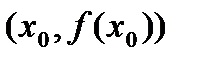 , выберем одну прямую — касательную к графику функции:
, выберем одну прямую — касательную к графику функции: 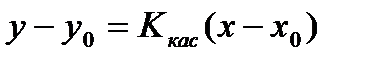 . Из геометрического смысла производной угловой коэффициент касательной:
. Из геометрического смысла производной угловой коэффициент касательной: 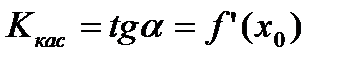 .
.
Þ 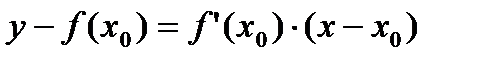 .
.
Þ 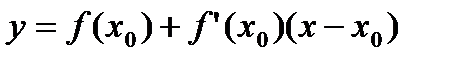 – уравнение касательной.
– уравнение касательной.
Определение: Нормалью к кривой называется прямая, перпендикулярная к касательной, проведенной в точке касания с абсциссой x0.
Так как нормаль перпендикулярна к касательной, то угловой коэффициент нормали: 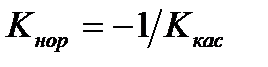 (из условия перпендикулярности прямых). Отсюда:
(из условия перпендикулярности прямых). Отсюда: 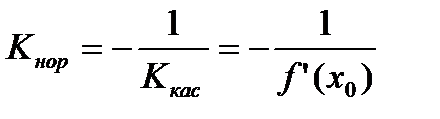 Þ
Þ 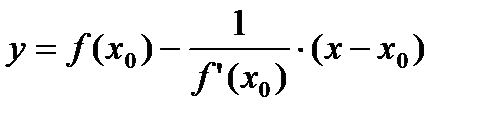 – уравнение нормали.
– уравнение нормали.
Пример: Составить уравнение касательной и нормали к графику функции 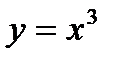 в точке с абсциссой равной 1.
в точке с абсциссой равной 1.
Ордината точки касания: 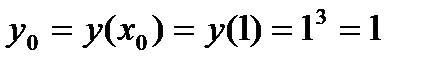
Производная: 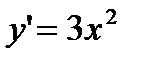 .
.
Найдем значение производной в точке x0: 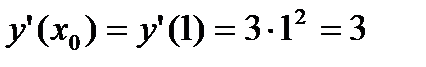
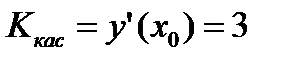 ,
, 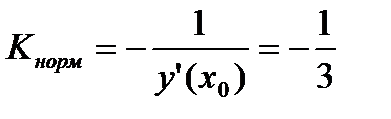
Уравнение касательной: 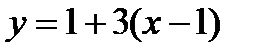 Þ
Þ 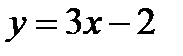
Уравнение нормали: 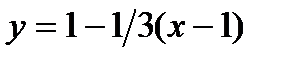 Þ
Þ 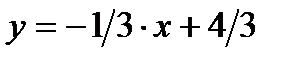 .
.
Дата добавления: 2015-08-11; просмотров: 2219;
