Производная функции, заданной параметрически.
Функция задана параметрически, если зависимость y от x осуществляется с помощью параметра t: 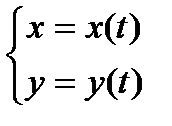 , где tÎT.
, где tÎT.
Пример: 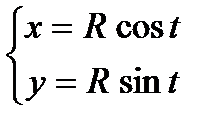 — параметрическое уравнение окружности с центром C(0,0) и радиусом R.
— параметрическое уравнение окружности с центром C(0,0) и радиусом R.
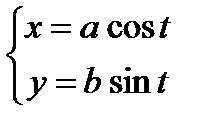 — параметрическое уравнение эллипса, где a и b большая и малая полуоси.
— параметрическое уравнение эллипса, где a и b большая и малая полуоси.
Вычисление производных функции, заданной параметрически:
Чтобы получить явную зависимость y от x, нужно из системы исключить параметр t. Для этого предполагаем, что для функции 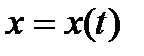 на промежутке t существует обратная функция
на промежутке t существует обратная функция 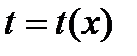 . Тогда
. Тогда 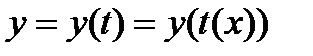 – сложная функция. Продифференцируем:
– сложная функция. Продифференцируем:  .
.
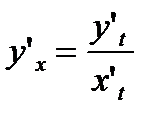 ;
;  .
.
Дата добавления: 2015-08-11; просмотров: 738;
