Момент инерции тела относительно параллельных осей

Теорема Гюйгенса. Моменты инерции данного тела относительно разных осей будут, в общем случае, разными. Зная J_С относительно одной оси, можно найти J_О относительно другой, ей параллельной.

Проведем оси 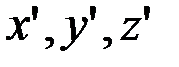через центр масс С и оси x, y, z, параллельные осям 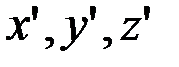, через произвольную точку O , лежащую на оси .

Пользуясь формулами (3), запишем:

.

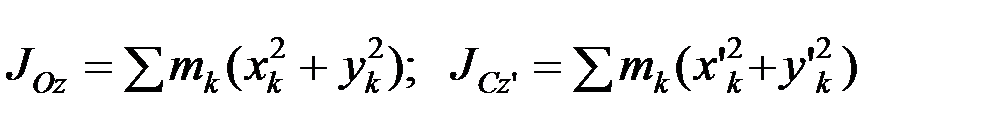Из рисунка видно, что

.

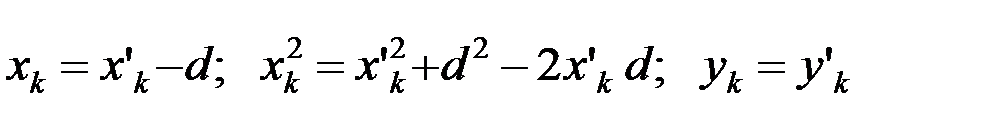Тогда

,

; ; .

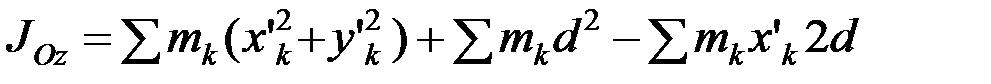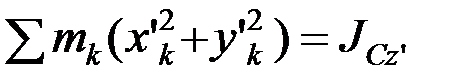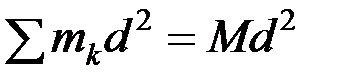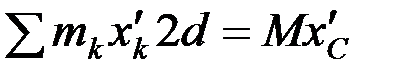Т.к. точка С является центром тяжести, то

Следовательно, третья сумма равна нулю, тогда

.

Итак, теорема Гюйгенса формулируется следующим образом: момент инерции тела относительно данной оси равен моменту инерции относительно центральной оси, ей параллельной, сложенному с произведением массы всего тела на квадрат расстояния между осями.

Очевидно, что 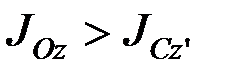, следовательно, момент инерции тела, относительно оси, проходящей через центр масс, будет наименьшим для всех осей данного направления.