Лекция 11 ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ (кинетический момент) системы относительно центра и оси

Понятие о моменте количества движения точки.
Теорема об изменении момента количества движения точки.
Кинетический момент. Теорема об изменении кинетического
момента системы при ее движении по отношению к центру масс

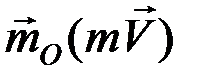Моментом количества движения точки относительно некоторого центра О называется векторная величина , определяемая равенством:

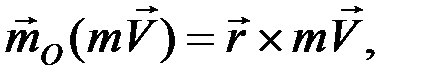(1)

где – радиус-вектор движущейся точки. Вектор 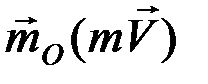направлен перпендикулярно плоскости, проходящей через 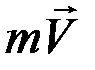и центр О, а модуль равен ,

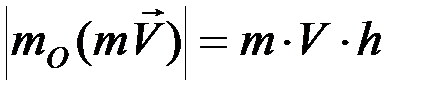где h – кратчайшее расстояние от центра до линии действия вектора скорости.

Момент количества движения (МКД) точки относительно какой-либо оси Оz , проходящей через центр О, равен проекции вектора 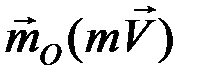на эту плоскость:

.

Продифференцируем обе части уравнения (1). Для правой части

.

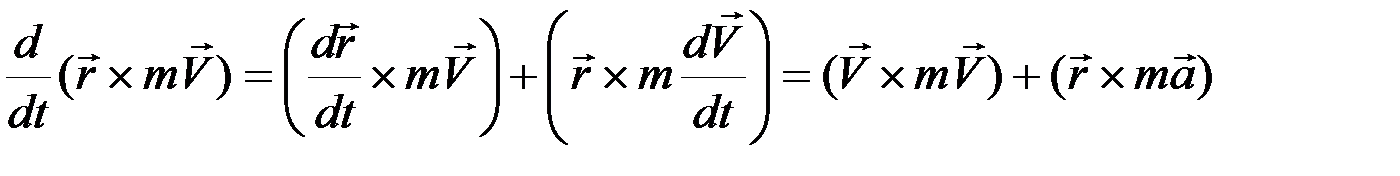Выражение 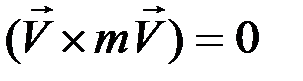как векторное произведение двух параллельных векторов. Учитывая, что – момент силы 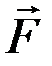относительно центра 0 , получим:

.

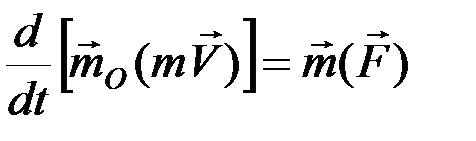Теорема об изменении момента количества движения точки.Производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра.