Закон сохранения момента количества движения точки
Из равенства следует, что если 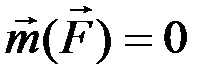 , то
, то 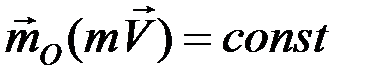 .
.
Если момент действующих сил относительно некоторого центра равен нулю, то момент количества движения точки относительно этого центра есть величина постоянная.
Такое возможно в двух случаях: либо 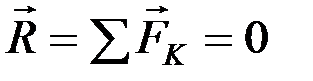 , либо плечо равно нулю, тогда эта сила будет называться центральной, т.е. линия ее действия проходит все время через данный центр О (например, сила притяжения планет к Солнцу, сила натяжения нити при кордовой модели).
, либо плечо равно нулю, тогда эта сила будет называться центральной, т.е. линия ее действия проходит все время через данный центр О (например, сила притяжения планет к Солнцу, сила натяжения нити при кордовой модели).
Главным моментом количеств движения (или кинетическим моментом) системы относительно данного центра О называется векторная величина 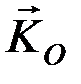 , равная геометрической сумме моментов количеств движения всех точек системы относительно этого центра:
, равная геометрической сумме моментов количеств движения всех точек системы относительно этого центра:
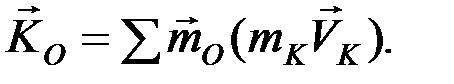
Аналогично определяются моменты количеств движения (МКД) относительно координатных осей:
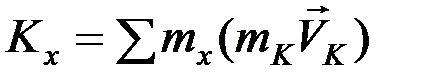 ,
,
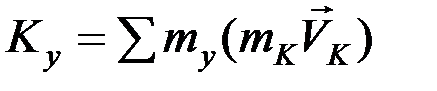 ,
,
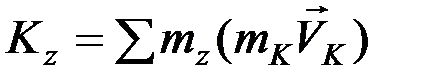 .
.
В предыдущей лекции отмечалось, что количество движения можно рассматривать как характеристику поступательного движения. Ниже покажем, что главный МКД системы может рассматриваться как характеристика вращательного движения.
Дата добавления: 2015-08-08; просмотров: 666;
