Определение скоростей и ускорений точек вращающегося тела. Скорости точек тела

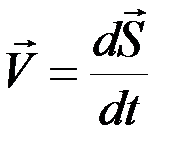Возьмем точку М тела на расстоянии h от оси вращения. Точка M будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения. Если за время dt происходит элементарный поворот dj, то ; скорость 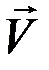называется линейной или окружной. Учитывая, что 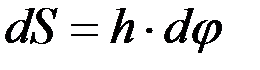, получим .

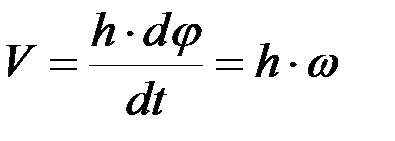Числовое значение скорости точки вращающегося тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения. Скорость направлена по касательной к описываемой окружности. Так как w для всех точек тела одинаковы, то скорости точек вращающегося тела пропорциональны их расстояниям до оси вращения.

Для определения ускорений точек тела воспользуемся формулами:

; .

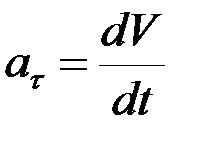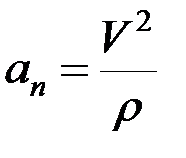В нашем случае ,

, .

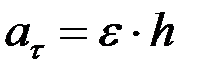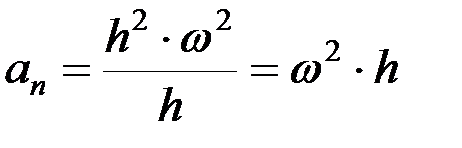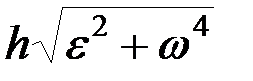Отклонение вектора полного ускорения от радиуса определяется углом :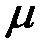

.

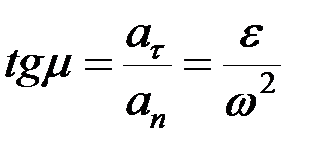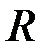Пример.Вал радиуса = 10 см приводится во вращение гирей, подвешенной к нему на нити. Движение гири выражается уравнением , где х – расстояние гири от места схода нити с поверхности вала, выражаемое в см, t – время, выражаемое в секундах. Определить угловую скорость w и угловое ускорение e вала, а также полное ускорение точки В на поверхности вала в момент времени t.

Решение:

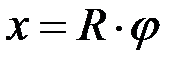, где j – угол поворота вала .

,

,

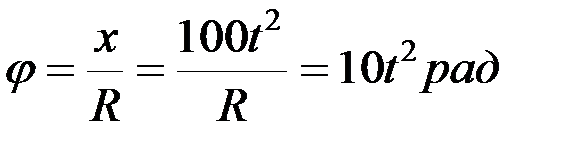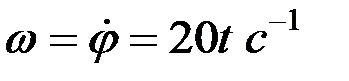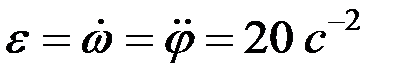см/с²,

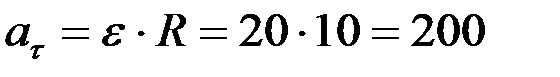см/с².

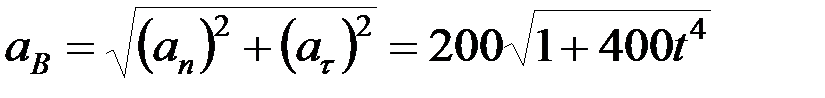см/с².

Лекция 6
ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА (определение скоростей)

Разложение плоского движения твердого тела на
поступательное и вращательное. Уравнение плоского движения.
Определение скоростей точек твердого тела. Теорема о скоростях точек
твердого тела, ее следствие. Определение скоростей точек твердого тела
с помощью мгновенного центра скоростей. План скоростей

Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой фиксированной плоскости.