Координаты центров тяжести однородных тел

Однородная материальная линия. Тело, у которого два измерения (высота и ширина) пренебрежимо малы по сравнению с третьим измерением (длиной), называют материальной линией (например, стержень). У таких тел отношение силы тяжести G к длине l – постоянная величина для любого произвольного участка линии:

.

С учётом этого выражения формулы для определения координат центра тяжести можно выразить так:

, , .

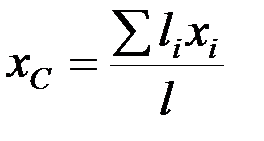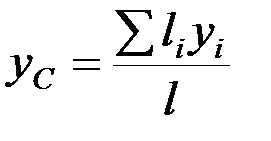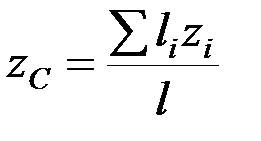Однородная материальная поверхность. Материальной поверхностью называют тело, у которого одно измерение (толщина) пренебрежимо мало по сравнению с двумя другими (длиной и шириной). У однородной материальной поверхности отношение силы тяжести к площади поверхности есть постоянная величина для любой произвольной части поверхности:

.

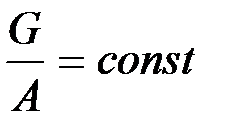Формулы для определения координат центра тяжести:

, , ,

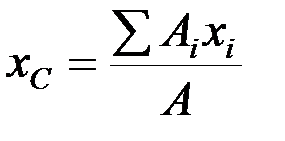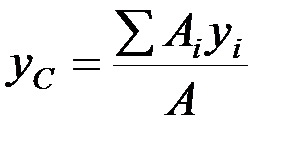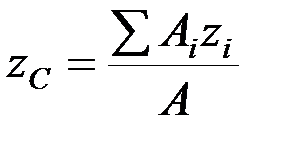где A – полная площадь поверхности.

Однородный материальный объем. Материальный объем имеет соизмеримыми все три измерения. Для любой части однородного тела

.

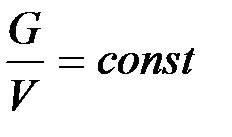Формулы для определения координат центра тяжести:

, , ,

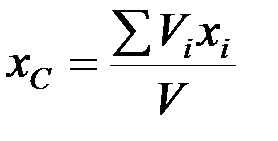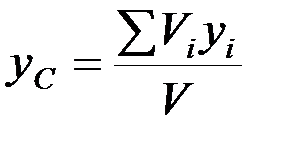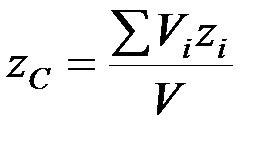где V — полный объем тела.

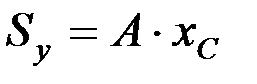Статический момент площади. Произведение площади фигуры A на расстояние от ее центра тяжести до какой-либо оси называют статическим моментом этой площади относительно данной оси. Так, – статический момент площади A относительно оси х, а – статический момент этой же площади относительно оси у. Чтобы определить статический момент площади сложной фигуры относительно некоторой оси, необходимо сложить статические моменты отдельных частей фигуры относительно этой же оси, т.е.

,

.

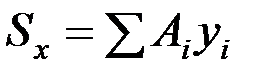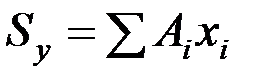Ось, проходящую через центр тяжести, называют центральной. Статический момент плоской фигуры относительно любой центральной оси равен нулю.

При решении задач на определение положения центра тела необходимо иметь в виду, что если однородное тело имеет плоскость симметрии, ось симметрии или центр симметрии, то его центр тяжести обязательно лежит в этой плоскости, на этой оси, в этом центре.

На практике часто необходимо определить положение центра тяжести тел, имеющих сложную форму. Для этого существуют два метода определения: метод группировок (разбивки) и метод отрицательных масс.

Первый метод заключается в том, что тело разбивается на наименьшее число простейших частей, силы тяжести которых и положение их центров тяжести известны, после чего применяют выведенные ранее формулы.

При использовании второго метода тела, имеющие свободные полости, считают сплошными, а массу свободных полостей считают отрицательной. Вид формул для определения координат центра тяжести при этом не меняется.