Векторно-координатный способ задания движения
Пусть закон движения задан радиус-вектором 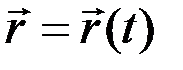 или равносильной ему системой трех скалярных координат:
или равносильной ему системой трех скалярных координат:

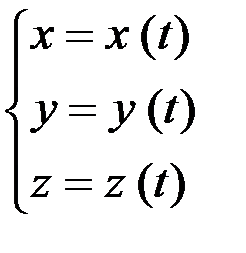 .
.
Допустим, в некоторый момент времени t положение точки m определяет 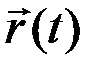 , а в следующий момент
, а в следующий момент 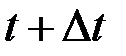 соответственно
соответственно 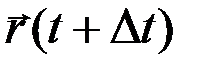 , тогда за время
, тогда за время 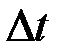 радиус-вектор получит приращение
радиус-вектор получит приращение 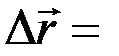
 '
' 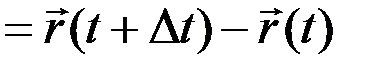 .
.
Вектор 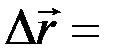
 ' называется вектором перемещения точки за
' называется вектором перемещения точки за 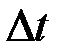 . Отношение вектора перемещения точки к соответствующему промежутку времени называется вектором средней скорости точки за промежуток времени
. Отношение вектора перемещения точки к соответствующему промежутку времени называется вектором средней скорости точки за промежуток времени 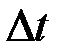 :
:
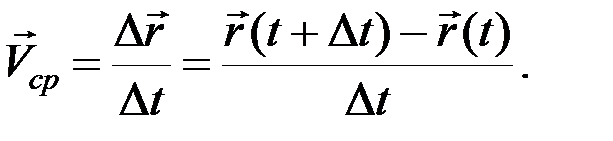

 Из уравнения следует, что
Из уравнения следует, что 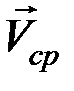 – вектор, направленный по хорде
– вектор, направленный по хорде 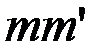 в сторону движения. Очевидно, чем меньше
в сторону движения. Очевидно, чем меньше 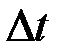 , тем точнее
, тем точнее 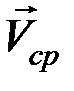 будет выражать скорость точки в момент времени
будет выражать скорость точки в момент времени 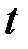 . Поэтому переходим в равенстве к пределу при Δt → 0.
. Поэтому переходим в равенстве к пределу при Δt → 0.
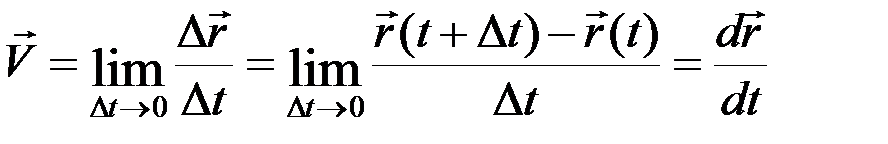 – векторная производная.
– векторная производная.
Скорость точки равна векторной производной от радиус-вектора точки по времени и направлена по касательной к ее траектории в сторону движения:
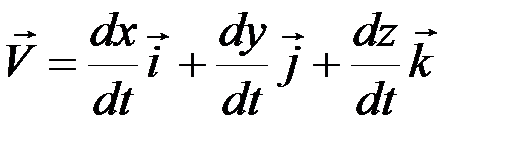
или
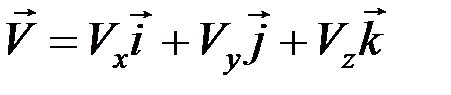 ,
,
где 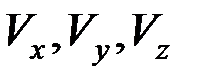 – проекции вектора скорости на координатные оси.
– проекции вектора скорости на координатные оси.
| При этом | 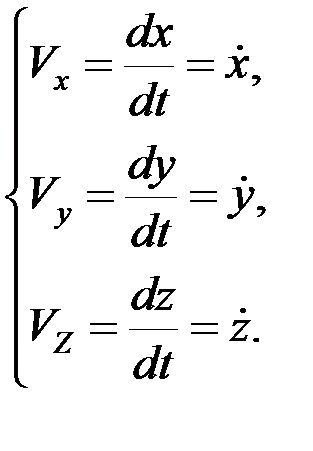
|
Складывая составляющие скорости, пролучим 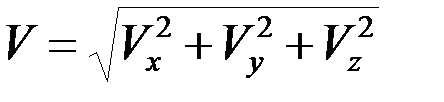 .
.
Таким образом, если движение точки задано системой уравнений (1), можно найти величину и направление скорости.
Дата добавления: 2015-08-08; просмотров: 1489;
