Естественный способ задания движения

Пусть движение точки m задано уравнением 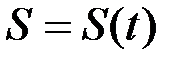. Требуется найти скорость точки. Пусть точка m определяется еще и радиус-вектором относительно точки O, тогда

.

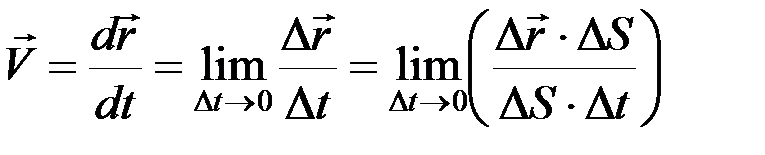Т.к. при 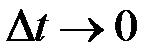, , 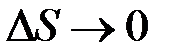то можно записать

.

Рассмотрим каждый предел в отдельности.

.

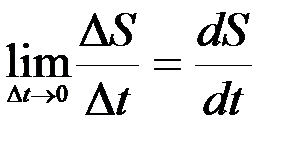Предел отношения направляющей хорды к стягивающей ею дуге по величине равен единице и направлен по касательной к траектории: 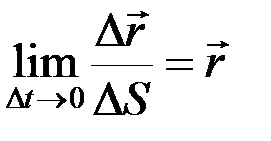(r = 1), тогда 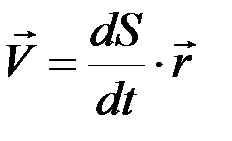, а алгебраическая величина скорости .

Единичный вектор направлен всегда в сторону возрастания дуговой координаты, поэтому при движении точки в сторону возрастания , а при движении в обратную сторону – .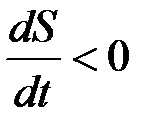

Скорость точки равна первой производной от дуговой координаты по времени и направлена по касательной к траектории точки в сторону ее движения.