Векторно-координатный способ задания движения точки
 Пусть точка m совершает движение по отношению к прямоугольной системе координат xyz. Для определения положения точки в этой системе необходимо знать три ее координаты
Пусть точка m совершает движение по отношению к прямоугольной системе координат xyz. Для определения положения точки в этой системе необходимо знать три ее координаты 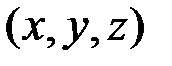 . Если эти координаты известны для любого момента времени, то движение точки считается заданным, то есть координаты заданы в виде известных функций времени:
. Если эти координаты известны для любого момента времени, то движение точки считается заданным, то есть координаты заданы в виде известных функций времени:

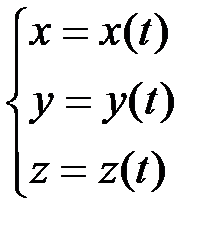 . (1)
. (1)
Система уравнений (1) представляет собой уравнения движения точки в декартовой системе координат.
Функции времени однозначны (точка в одно и то же время не может находиться в других точках пространства), непрерывны (бесконечно малому приращению времени t соответствует бесконечно малое приращение координат) и должны допускать производные. Положение точки m в пространстве может быть определено радиусом-вектором 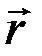 , определяющим ее положение относительно некоторой точки пространства:
, определяющим ее положение относительно некоторой точки пространства: 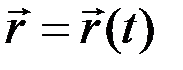 . Приняв за начало радиуса-вектора
. Приняв за начало радиуса-вектора 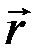 начало координат системы xyz, всегда можно выразить
начало координат системы xyz, всегда можно выразить 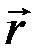 через его проекции на оси координат:
через его проекции на оси координат:
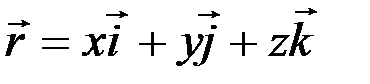 ,
,
где 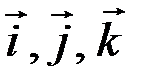 – единичные орты координатных осей;
– единичные орты координатных осей;
x, y, z – координаты точки m, равные проекциям вектора 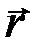 на соответствующие оси.
на соответствующие оси.
Величина радиуса вектора равна 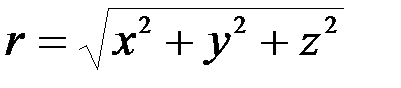 , а направление его определяют направляющие косинусы:
, а направление его определяют направляющие косинусы:
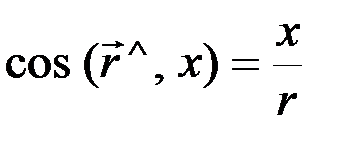 ;
; 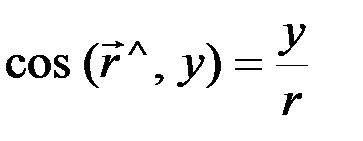 ;
; 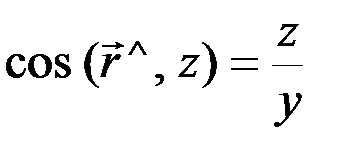 .
.
Очевидно, если задана система уравнений (1), то можно определить 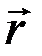 , и наоборот. Уравнения (1) могут рассматриваться как параметрические с параметром t. При переходе от параметрических уравнений к уравнениям, связывающим координаты (путем исключения параметра t), получают уравнение траектории точки. Например, из первого уравнения выразим
, и наоборот. Уравнения (1) могут рассматриваться как параметрические с параметром t. При переходе от параметрических уравнений к уравнениям, связывающим координаты (путем исключения параметра t), получают уравнение траектории точки. Например, из первого уравнения выразим 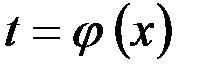 и подставим в остальные:
и подставим в остальные:
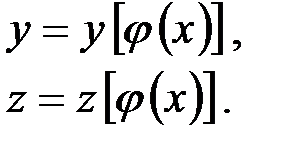
Эти уравнения дают траекторию точки в виде линии пересечения двух поверхностей.
Дата добавления: 2015-08-08; просмотров: 995;
