Векторно-координатный способ задания движения. Пусть движение точки m задано уравнением или системой уравнений
Пусть движение точки m задано уравнением 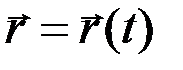 или системой уравнений
или системой уравнений 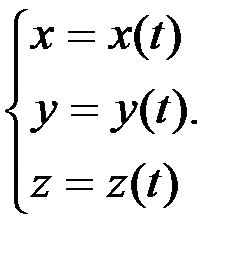
 Если в момент времени t точка m имеет скорость
Если в момент времени t точка m имеет скорость 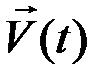 , то в следующий момент
, то в следующий момент 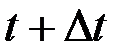 ее скорость –
ее скорость – 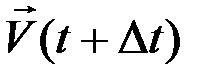 .
.
Тогда 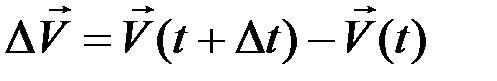 .
.
Перенесем вектор 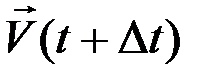 из точки m' в точку m
из точки m' в точку m  и построим параллелограмм. Тогда
и построим параллелограмм. Тогда 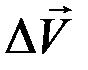 будет его стороной. Отношение приращения
будет его стороной. Отношение приращения 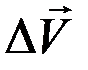 к промежутку времени
к промежутку времени 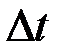 называется средним ускорением точки m за время
называется средним ускорением точки m за время 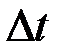 :
:
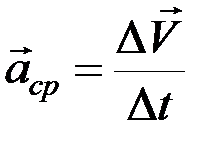 .
.
Очевидно, что вектор 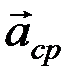 направлен по вектору
направлен по вектору 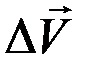 . Ускорением точки в данный момент времени t называется предел, к которому стремится вектор среднего ускорения при
. Ускорением точки в данный момент времени t называется предел, к которому стремится вектор среднего ускорения при 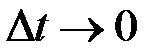 :
:
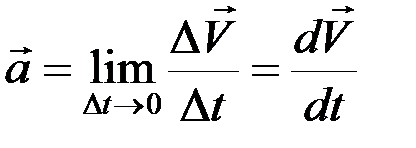 .
.
Ускорение точки равно производной от вектора ее скорости по времени. Вспомнив, что 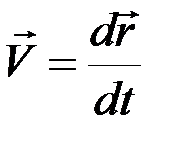 , получим
, получим 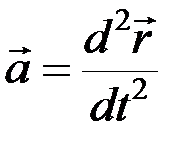 .
.
Чтобы найти величину и направление вектора ускорения аналитически, представим радиус-вектор через его проекции:
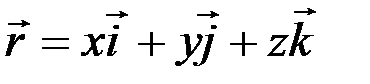 .
.
Тогда 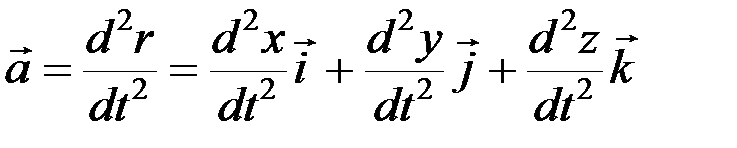 или
или 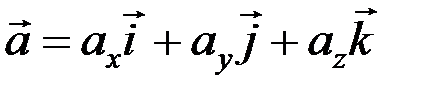 .
.
Сравнивая эти равенства, получим:
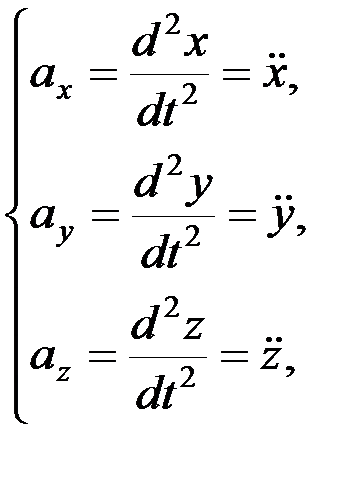
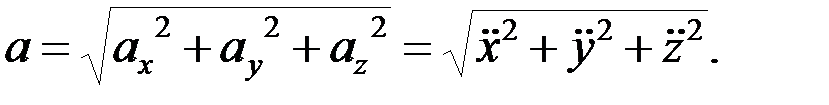
Дата добавления: 2015-08-08; просмотров: 1565;
