Индуктивность в цепи переменного тока

Переменный ток, протекающий через индуктивность, описывается следующим выражением:

i = I_m · sin ωt ; ;

Ф = Ф_m · sin ωt ;

При протекании этого тока в катушке индуктивности создается переменный магнитный поток, который совпадает по фазе с протекающим током:

Под воздействием переменного магнитного поля в катушке появляется э.д.с. самоиндукции:

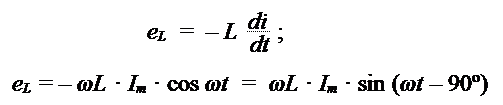Сомножитель ωL имеет размерность сопротивления и представляет собой реактивное сопротивление x_L катушки индуктивности:

x_L = ωL = 2π f L ;

Поэтому ωL · I_m = x_L · I_m = E_m ;

e_L = – E_m · cos ωt = E _m· sin (ωt – 90º) ; ;

Следовательно, э.д.с. самоиндукции отстает по фазе от тока на 90º.

Для поддержания тока в катушке к ней должно быть приложено напряжение u от источника переменного тока, которое в любой момент времени по величине равно э.д.с. самоиндукции, и имеет знак, противоположный знаку э.д.с. самоиндукции:

u = – e_L ;

u = – E _m · sin (ωt – 90º);

После преобразования получаем:

u = U _m · sin (ωt + 90º) ;

Таким образом, напряжение, приложенное к катушке индуктивности, опережает протекающий ток на 90º.

В реальных условиях катушка индуктивности имеет не только реактивное сопротивление ωL, но и активное R. Эквивалентная схема реальной катушки индуктивности приведена на рис. 3.1.3.

Рис. 3.1.3. Эквивалентная схема катушки индуктивности

Векторные диаграммы напряжений и сопротивлений для реальной катушки индуктивности приведены на рис. 3.1.4.

При построении диаграммы напряжений за исходный вектор принят вектор тока I, т. к. его значение одинаково для всей последовательной цепи.

Рис. 3.1.4. Векторные диаграммы катушки индуктивности

a) диаграмма токов и напряжений; b) диаграмма сопротивлений.

Падение напряжения на активном сопротивлении равно:

U_R = I · R ;

Это напряжение совпадает по фазе с протекающим током I. Падение напряжения на индуктивном сопротивлении U_L = I · w L опережает по фазе ток I на 90º. Суммарное напряжение U является геометрической суммой напряжений U_R и U_L :

Разделив обе части уравнения на I, получим выражение для общего сопротивления цепи:

Сдвиг фаз φ между напряжением и током определяется из выражения:

<11 12 131415 16 17 >

Дата добавления: 2015-08-08; просмотров: 1213;