Глава 3. Статистический анализ экспериментальных данных
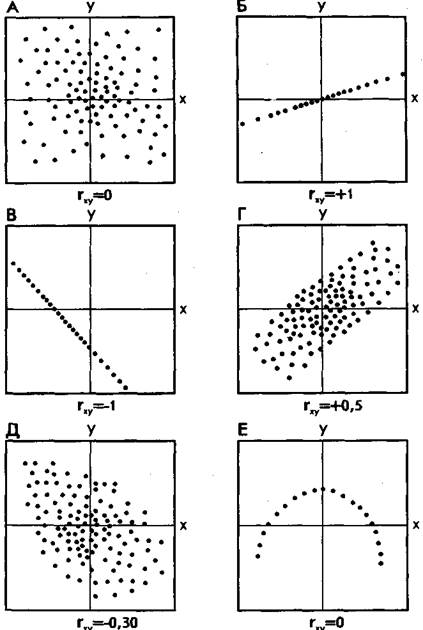
Рис. 74. Схематическое представление различных корреляционных зависимостей с соответствующими значениями коэффициента линейной корреляции (цит. по: Шерла К. Факторный анализ. М, 1980).
______ Часть II. Введение в научное психологическое исследование___
Наконец, фрагмент Е дает коэффициент корреляции, равный или близкий к 0, так как в данном случае связь между переменными хотя и существует, но не является линейной.
Коэффициент линейной корреляции определяется при помощи следующей формулы:
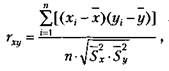
где г — коэффициент линейной корреляции;
х, у — средние выборочные значения сравниваемых величин; х., у — частные выборочные значения сравниваемых величин; п — общее число величин в сравниваемых рядах показателей;
si' Sy ~ дисперсии, отклонения сравниваемых величин от
средних значений.
Пример.Определим коэффициент линейной корреляции между следующими двумя рядами показателей. Ряд 1:2,4,4,5,3, 6, 8. Ряд II: 2, 5, 4, 6, 2, 5, 7. Средние значения этих двух рядов соответственно равны 4,6 и 4,4. Их дисперсии составляют следующие величины: 3,4 и 3,1. Подставив эти данные в приведенную выше формулу коэффициента линейной корреляции, получим следующий результат: 0,92. Следовательно, между рядами данных существует значимая связь, причем довольно явно выраженная, так как коэффициент корреляции близок к единице. Действительно, взглянув на эти ряды цифр, мы обнаруживаем, что большей цифре в одном ряду соответствует большая цифра в другом ряду и, наоборот, меньшей цифре в одном ряду соответствует примерно такая же малая цифра в другом ряду.
К коэффициенту ранговой корреляции в психолого-педагогических исследованиях обращаются в том случае, когда признаки, между которыми устанавливается зависимость, являются качественно различными и не могут быть достаточно точно оценены при помощи так называемой интервальной измерительной шкалы. Интервальной называют такую шкалу, которая позволяет оценивать расстояния между ее значениями и судить о
______ Глава 3. Статистический анализ экспериментальных данных___
том, какое из них больше и насколько больше другого. Например, линейка, с помощью которой оцениваются и сравниваются длины объектов, является интервальной шкалой, так как, пользуясь ею, мы можем утверждать, что расстояние между двумя и шестью сантиметрами в два раза больше, чем расстояние между шестью и восемью сантиметрами. Если же, пользуясь некоторым измерительным инструментом, мы можем только утверждать, что одни показатели больше других, но не в состоянии сказать на сколько, то такой измерительный инструмент называется не интервальным, а порядковым.
Большинство показателей, которые получают в психолого-педагогических исследованиях, относятся к порядковым, а не к интервальным шкалам (например, оценки типа «да», «нет», «скорее нет, чем да» и другие, которые можно переводить в баллы), поэтому коэффициент линейной корреляции к ним неприменим. В этом случае обращаются к использованию коэффициента ранговой корреляции, формула которого следующая:
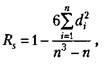
где Rs — коэффициент ранговой корреляции по Спирмену;
di — разница между рангами показателей одних и тех же испытуемых в упорядоченных рядах;
п — число испытуемых или цифровых данных (рангов) в коррелируемых рядах.
Пример.Допустим, что педагога-экспериментатора интересует, влияет ли интерес учащихся к учебному предмету на их успеваемость. Предположим, что с помощью некоторой психодиагностической методики удалось измерить величину интереса к учению и выразить его для десяти учащихся в следующих цифрах: 5,6,7,8,2,4,8,7,2,9. Допустим также, что при помощи другой методики были определены средние оценки этих же учащихся по данному предмету, оказавшиеся соответственно равными: 3,2; 4,0; 4,1; 4,2; 2,5; 5,0; 3,0; 4,8; 4,6; 2,4.
Упорядочим оба ряда оценок по величине цифр и припишем каждому из учащихся по два ранга; один из них указывает на то,
19* 579
______ Часть II. Введение в научное психологическое исследование____
какое место среди остальных данных ученик занимает по успеваемости, а другой — на то, какое место среди них же он занимает по интересу к учебному предмету. Ниже приведены ряды цифр, два из которых (первый и третий) представляют исходные данные, а два других (второй и четвертый) — соответствующие ранги1:
| 2-1,5 | 2,4-1 |
| 2-1,5 | 2,5-2 |
| 4-3 | 3,0-3 |
| 5-4 | 3,2 - 4 |
| 6-5 | 4,0-5 |
| 7-6,5 | 4,1-6 |
| 7-6,5 | 4,2-7 |
| 8-8,5 | 4,6-8 |
| 9-10 | 5,0 - 10 |
Определив сумму квадратов различий в рангах ( ^df ) и подставив нужное значение в числитель формулы, получаем, что коэффициент ранговой корреляции равен 0,97, т.е. достаточно высок, что и говорит о том, что между интересом к учебному предмету и успеваемостью учащихся действительно существует статистически достоверная зависимость.
Однако по абсолютным значениям коэффициентов корреляции не всегда можно делать однозначные выводы о том, являются ли они значимыми, т.е. достоверно свидетельствуют о существовании зависимости между сравниваемыми переменными. Может случиться так, что коэффициент корреляции, равный 0,50, не будет достоверным, а коэффициент корреляции, составивший 0,30, — достоверным. Многое в решении этого вопроса зависит от того, сколько показателей было в коррелируемых друг с другом рядах признаков: чем больше таких показателей, тем меньшим по величине может быть статистически достоверный коэффициент корреляции.
В табл. 35 представлены критические значения коэффициентов корреляции для различных степеней свободы. (В данном
1 Если исходные данные, которые ранжируются, одинаковы, то и их ранги также будут одинаковыми. Они получаются путем суммирования и деления пополам тех рангов, которые соответствуют этим данным.
Глава 3. Статистический анализ экспериментальных данных___
Таблица 35 Критические значения коэффициентов корреляции для различных степеней свободы (и - 2) и разных вероятностей допустимых ошибок
| Число | |||
| степеней свободы | Уровень значимости | [ | |
| 0,05 | 0,01 | 0,001 | |
| 0,9500 | 0,9900 | 0,9900 | |
| 0,7545 | 0,8745 | 0,9509 | |
| 0,5760 | 0,7079 | 0,8233 | |
| И | |||
| 0,4821 | 0,6055 | 0,7247 | |
| 0,4227 | 0,5368 | 0,6524 | |
| 0,3809 | 0,4869 | 0,5974 | |
| 28 , | |||
| 0,3494 | 0,4487 | 0,5541 | |
| 0,3338 | 0,4297 | 0,5322 | |
| 0,3246 | 0,4182 | 0,5189 | |
| 0,3044 | 0,3932 | 0,4896 |
Часть II. Введение в научное психологическое исследование
случае степенью свободы будет число, равное и — 2, где п — количество данных в коррелируемых рядах.) Заметим, что значимость коэффициента корреляции зависит и от заданного уровня значимости или принятой вероятности допустимой ошибки в расчетах. Если, к примеру, коррелируется друг с другом два ряда цифр по 10 единиц в каждом и получен коэффициент корреляции между ними, равный 0,65, то он будет значимым на уровне 0,95 (он больше критического табличного значения, составляющего 0,6319 для вероятности допустимой ошибки 0,05, и меньше критического значения 0,7646 для вероятности допустимой ошибки 0,01).
Метод множественных корреляций в отличие от метода парных корреляций позволяет выявить общую структуру корреляционных зависимостей, существующих внутри многомерного экспериментального материала, включающего более двух переменных, и представить эти корреляционные зависимости в виде некоторой системы.
Один из наиболее распространенных вариантов этого метода — факторный анализ — позволяет определить совокупность внутренних взаимосвязей, возможных причинно-следственных связей, существующих в экспериментальном материале. В результате факторного анализа обнаруживаются так называемые факторы — причины, объясняющие множество частных (парных) корреляционных зависимостей.
Фактор — математико-статистическое понятие. Будучи переведенным на язык психологии (эта процедура называется содержательной или психологической интерпретацией факторов), он становится психологическим понятием. Например, в известном 16-факторном личностном тесте Р. Кеттела, который подробно рассматривался в первой части книги, каждый фактор взаимно однозначно связан с определенными чертами личности человека.
С помощью выявленных факторов объясняют взаимозави-. симость психологических явлений. Поясним сказанное на примере. Допустим, что в некотором психолого-педагогическом эксперименте изучалось взаимовлияние таких переменных, как характер, способности, потребности и успеваемость учащихся. Предположим далее, что, оценив каждую из этих переменных у
Глава 3. Статистический анализ экспериментальных данных
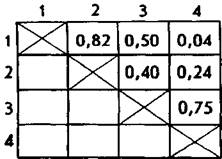
достаточно представительной выборки испытуемых и подсчитав коэффициенты парных корреляций между всевозможными парами данных переменных, мы получили следующую матрицу интеркорреляций (в ней справа и сверху цифрами обозначены в перечисленном выше порядке изученные в эксперименте переменные, а внутри самого квадрата показаны их корреляции друг с другом; поскольку всевозможных пар в данном случае меньше, чем клеток в матрице, то заполнена только верхняя часть матрицы, расположенная выше ее главной диагонали).
|
Анализ корреляционной матрицы показывает, что переменная 1 (характер) значимо коррелирует с переменными 2 и 3 (способности и потребности). Переменная 2 (способности) достоверно коррелирует с переменной 3 (потребности), а переменная 3 (потребности) — с переменной 4 (успеваемость). Фактически из шести имеющихся в матрице коэффициентов корреляции четыре являются достаточно высокими и, если предположить, что они определялись на совокупности испытуемых, превышающей 10 человек, — значимыми.
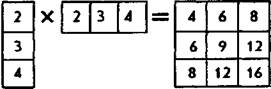
Зададим некоторое правило умножения столбцов цифр на строки матрицы: каждая цифра столбца последовательно умножается на каждую цифру строки и результаты парных произведений записываются в строку аналогичной матрицы. Пример: если по этому правилу умножить друг на друга три цифры столбца и строки, представленные в левой части матричного равенства, то получим матрицу, находящуюся в правой части этого же равенства:
Часть II. Введение в научное психологическое исследование
Задача факторного анализа по отношению к только что рассмотренной является как бы противоположной. Она сводится к тому, чтобы по уже имеющейся матрице парных корреляций, аналогичной представленной в правой части показанного выше матричного равенства, отыскать одинаковые по включенным в них цифрам столбец и строку, умножение которых друг на друга по заданному правилу порождает корреляционную матрицу. Иллюстрация:
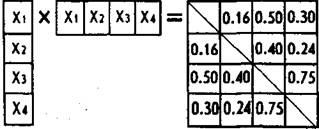
Здесь xv ху х3 и хА — искомые числа. Для их точного и быстрого определения существуют специальные математические процедуры и программы для ЭВМ.
Допустим, что мы уже нашли эти цифры: хх = 0,45, х2= 0,36 х3 - 1,12, х4 = 0,67. Совокупность найденных цифр и называется фактором, а сами эти цифры — факторными весами или нагрузками.
Эти цифры соответствуют тем психологическим переменным, между которыми вычислялись парные корреляции. хх — характер, х2 — способности, х3 — потребности, х4 — успеваемость. Поскольку наблюдаемые в эксперименте корреляции между переменными можно рассматривать как следствие влияния на них общих причин — факторов, а факторы интерпретируются в психологических терминах, мы можем теперь от факторов перейти к содержательной психологической интерпретации обнаруженных статистических закономерностей. Фактор содержит в себе ту же самую информацию, что и вся корреляционная матрица, а факторные нагрузки соответствуют коэффициентам корреляции. В нашем примере х3 (потребности) имеет наибольшую факторную нагрузку (1,12), а х, (способности) — наименьшую (0,36).
Глава 3. Статистический анализ экспериментальных данных
Следовательно, наиболее значимой причиной, влияющей на все остальные психологические переменные, в нашем случае являются потребности, а наименее значимой — способности. Из корреляционной матрицы видно, что связи переменной х3 со всеми остальными являются наиболее сильными (от 0,40 до 0,75), а корреляции переменной х2 — самыми слабыми (от 0,16 до 0,40).
Чаще всего в итоге факторного анализа определяется не один, а несколько факторов, по-разному объясняющих матрицу интеркорреляций переменных. В таком случае факторы делят на генеральные, общие и единичные. Генеральными называются факторы, все факторные нагрузки которых значительно отличаются от нуля (нуль нагрузки свидетельствует о том, что данная переменная никак не связана с остальными и не оказывает на них никакого влияния в жизни). Общие — это факторы, у которых часть факторных нагрузок отлична от нуля. Единичные — это факторы, в которых существенно отличается от нуля только одна из нагрузок. На рис. 75 схематически представлена структура факторного отображения переменных в факторах различной степени общности.
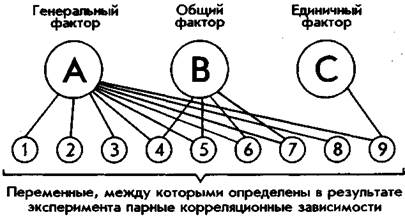
Рис. 75. Структура факторного отображения взаимосвязей переменных.
Отрезки, соединяющие факторы с переменными, указывают на высокие
факторные нагрузки
Часть II. Введение в научное психологическое исследование
Дата добавления: 2015-08-08; просмотров: 1181;
