МЕТОДЫ ВТОРИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
С помощью вторичных методов статистический обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, чем методы первичной статистической обработки, и требуют от исследователя хорошей подготовки в области элементарной математики и статистики.
Обсуждаемую группу методов можно разделить на несколько подгрупп: 1. Регрессионное исчисление. 2. Методы сравнения между собой двух или нескольких элементарных статистик (средних, дисперсий и т.п.), относящихся к разным выборкам. 3. Методы установления статистических взаимосвязей между переменными, например их корреляции друг с другом. 4. Методы выявления внутренней статистической структуры эмпирических данных (например, факторный анализ). Рассмотрим каждую из выделенных подгрупп методов вторичной статистической обработки на примерах.
Регрессионное исчисление — это метод математической статистики, позволяющий свести частные, разрозненные данные к некоторому линейному графику, приблизительно отражающему их внутреннюю взаимосвязь, и получить возможность по значению одной из переменных приблизительно оценивать вероятное значение другой переменной.
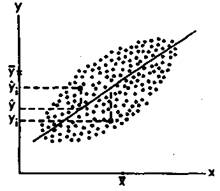
Воспользуемся для графического представления взаимосвязанных значений двух переменных х и у точками на графике (рис. 73). Поставим перед собой задачу: заменить точки на графике линией прямой регрессии, наилучшим образом представляющей взаимосвязь, существующую между данными переменными. Иными словами, задача заключается в том, чтобы через скопление точек, имеющихся на этом графике, провести прямую линию,
|
| ______ Глава 3. Статистический анализ экспериментальных данных____ |
Рис.73. Прямая регрессии YnoX. х и у — средние значения переменных. Отклонения отдельных значений от линии регрессии обозначены вертикальными пунктирными линиями. Величина yt - у является отклонением измеренного значения переменной у. от оценки, а величина у - у является отклонением оценки от среднего значения (Цит. по: Иберла К. Факторный анализ. М., 1980. С. 23).
пользуясь которой по значению одной из переменных, х или у, можно приблизительно судить о значении другой переменной. Для того чтобы решить эту задачу, необходимо правильно найти коэффициенты а и Ь в уравнении искомой прямой:
у = ах + Ь.
Это уравнение представляет прямую на графике и называется уравнением прямой регрессии.
Формулы для подсчета коэффициентов а и Ь являются следующими:
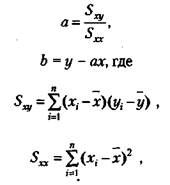
Часть II. Введение в научное психологическое исследование
где х., у{ — частные значения переменных X и Y, которым соответствуют точки на графике;
х, у — средние значения тех же самых переменных;
п — число первичных значений или точек на графике.
Для сравнения выборочных средних величин, принадлежащих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга, нередко используют ^-критерий Стъюдента. Его основная формула выглядит следующим образом:
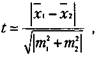
где х{ — среднее значение переменной по одной выборке данных;
хг — среднее значение переменной по другой выборке данных;
т1ит2 — интегрированные показатели отклонений частных значений из двух сравниваемых выборок от соответствующих им средних величин.
/и, и т2 в свою очередь вычисляются по следующим формулам:
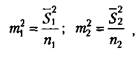
—2
где St — выборочная дисперсия первой переменной (по первой выборке);
—2
5"г — выборочная дисперсия второй переменной (по второй выборке);
я, — число частных значений переменной в первой выборке;
п2 — число частных значений переменной по второй выборке.
После того как при помощи приведенной выше формулы вычислен показатель t, по таблице 32 для заданного числа степеней свободы, равного п{ + п2 - 2, и избранной вероятности допустимой ошибки1 находят нужное табличное значение t и сравнива-
1 Степени свободы и вероятность допустимой ошибки — специальные ма-тематико-статистические термины, содержание которых мы здесь не будем рассматривать.
Глава 3. Статистический анализ экспериментальных данных
Таблица 32 Критические значения ^-критерия Стъюдента для заданного числа степеней свободы и вероятностей допустимых ошибок, равных 0,05; 0,01 и 0,001
| Число степеней свободы | Вероятность допустимой ошибки | ||
| 0,05 0,01 0,001 | |||
| Критические значения показателя t | |||
| (я, + п., - 2) | |||
| 2,78 | 5,60 | 8,61 | |
| 2,58 | 4,03 | 6,87 | |
| 2,45 | 3,71 | 5,96 | |
| 2,37 | 3,50 | 5,41 | |
| 2,31 | 3,36 | 5,04 | |
| 2,26 | 3,25 | 4,78 | |
| 2,23 | 3,17 | 4,59 | |
| 2,20 | 3,11 | 4,44' | |
| 2,18 | 3,05 | 4,32 | |
| 2,16 | 3,01 | 4,22 | |
| 2,14 | 2,98 | 4,14 | |
| 2,13 | 2,96 | 4,07 | |
| 2,12 | 2,92 | 4,02 | |
| 2,11 | 2,90 | 3,97 | |
| 2,10 | 2,88 | 3,92 | |
| 2,09 | 2,86 | 3,88 | |
| 2,09 | 2,85 | 3,85 | |
| 2,08 | 2,83 | 3,82 | |
| 2,07 | 2,82 | 3,79 | |
| 2,07 | 2,81 | 3,77 | |
| 2,06 | 2,80 | 3,75 | |
| 2,06 | 2,79 | 3,73 | |
| 2,06 | 2,78 | 3,71 | |
| 2,05 | 2,77 | 3,69 | |
| 2,05 | 2,76 | 3,67 | |
| 2,05 | 2,76 | 3,66 | |
| 2,04 | 2,75 | 3,65 | |
| 2,02 | 2,70 | 3,55 | |
| 2,01 | 2,68 | 3,50 | |
| 2,00 | 2,66 | 3,46 | |
| 1,99 | 2,64 | 3,42 | |
| 1,98 | 2,63 | 3,39 |
ют с ними вычисленное значение t. Если вычисленное значение t больше или равно табличному, то делают вывод о том, что сравниваемые средние значения из двух выборок действительно ста-
______ Часть II. Введение в, научное психологическое исследование___
тистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной. Рассмотрим процедуру вычисления t-критерия Стъюдента и определения на его основе разницы в средних величинах на конкретном примере.
Допустим, что имеются следующие две выборки экспериментальных данных: 2, 4, 5, 3, 2, 1, 3, 2, 6, 4 и 4, 5, 6, 4, 4, 3, 5, 2, 2, 7. Средние значения по этим двум выборкам соответственно равны 3,2 и 4,2. Кажется, что они существенно друг от друга отличаются. Но так ли это и насколько статистически достоверны эти различия? На данный вопрос может точно ответить только статистический анализ с использованием описанного статистического критерия. Воспользуемся этим критерием.
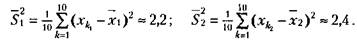
|
| Поставим найденные значения дисперсий в формулу для подсчета mat к вычислим показатель t |
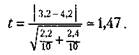
|
Определим сначала выборочные дисперсии для двух сравниваемых выборок значений:
Сравним его значение с табличным для числа степеней свободы 10+10-2 = 18. Зададим вероятность допустимой ошибки, равной 0,05, и убедимся в том, что для данного числа степеней свободы и заданной вероятности допустимой ошибки значение t должно быть не меньше чем 2,10. У нас же этот показатель оказался равным 1,47, т.е. меньше табличного. Следовательно, гипотеза о том, что выборочные средние, равные в нашем случае 3,2 и 4,2, статистически достоверно отличаются друг от друга, не подтвердилась, хотя на первый взгляд казалось, что такие различия существуют.
Вероятность допустимой ошибки, равная и меньшая чем 0,05, считается достаточной для научно убедительных выводов. Чем меньше эта вероятность, тем точнее и убедительнее делаемые выводы. Например, избрав вероятность допустимой ошибки, рав-
Глава 3. Статистический анализ экспериментальных данных
ную 0,05, мы обеспечиваем точность расчетов 95% и допускаем ошибку, не превышающую 5%, а выбор вероятности допустимой ошибки 0,001 гарантирует точность расчетов, превышающую 99,99%, или ошибку, меньшую чем 0,01%.
Описанная методика сравнения средних величин по критерию Стъюдента в практике применяется тогда, когда необходимо, например, установить, удался или не удался эксперимент, оказал или не оказал он влияние на уровень развития того психологического качества, для изменения которого предназначался. Допустим, что в некотором учебном заведении вводится новая экспериментальная программа или методика обучения, рассчитанная на то, чтобы улучшить знания учащихся, повысить уровень их интеллектуального развития. В этом случае выясняется причинно-следственная связь между независимой переменной — программой или методикой и зависимой переменной — знаниями или уровнем интеллектуального развития. Соответствующая гипотеза гласит: «Введение новой учебной программы или методики обучения должно будет существенно улучшить знания или повысить уровень интеллектуального развития учащихся».
Предположим, что данный эксперимент проводится по схеме, предполагающей оценки зависимой переменной в начале и в конце эксперимента. Получив такие оценки и вычислив средние по всей изученной выборке испытуемых, мы можем воспользоваться критерием Стъюдента для точного установления наличия или отсутствия статистически достоверных различий между средними до и после эксперимента. Если окажется, что они действительно достоверно различаются, то можно будет сделать определенный вывод о том, что эксперимент удался. В противном случае нет убедительных оснований для такого вывода даже в том случае, если сами средние величины в начале и в конце эксперимента по своим абсолютным значениям различны.
Иногда в процессе проведения эксперимента возникает специальная задача сравнения не абсолютных средних значений некоторых величин до и после эксперимента, а частотных, например процентных, распределений данных. Допустим, что для экспериментального исследования была взята выборка из 100 уча-
______ Часть II. Введение в научное психологическое исследование___
щихся и с ними проведен формирующий эксперимент. Предположим также, что до эксперимента 30 человек успевали на «удовлетворительно», 30 — на «хорошо», а остальные 40 — на «отлично». После эксперимента ситуация изменилась. Теперь на «удовлетворительно» успевают только 10 учащихся, на «хорошо» — 45 учащихся и на «отлично» — остальные 45 учащихся. Можно ли, опираясь на эти данные, утверждать, что формирующий эксперимент, направленный на улучшение успеваемости, удался? Для ответа на данный вопрос можно воспользоваться статистикой, называемой х2-критерий («хи-квадрат критерий»). Его формула выглядит следующим образом:
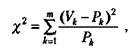
где Рк — частоты результатов наблюдений до эксперимента;
Vk — частоты результатов наблюдений, сделанных после эксперимента;
т — общее число групп, на которые разделились результаты наблюдений.
Воспользуемся приведенным выше примером для того, чтобы показать, как работает хи-квадрат критерий. В данном примере переменная Рк принимает следующие значения: 30%, 30%, 40%, а переменная Vk — такие значения: 10%, 45%, 45%.
Подставим все эти значения в формулу для %2 и определим его величину:
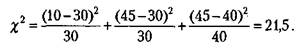
Воспользуемся теперь таблицей 33, где для заданного числа степеней свободы можно выяснить степень значимости образовавшихся различий до и после эксперимента в распределении оценок. Полученное нами значение х2 = 21,5 больше соответствующего табличного значения т - 1 = 2 степеней свободы, составляющего 13,82 при вероятности допустимой ошибки меньше чем 0,001. Следовательно, гипотеза о значимых изменениях, которые произошли в оценках учащихся в результате введения новой программы или новой методики обучения, эксперимен-
Глава 3, Статистический анализ экспериментальных данных___
Таблица 33 Граничные (критические) значения х2-критерия, соответствующие разным вероятностям допустимой ошибки и разным степеням свободы
| Число | |||
| степеней свободы | Вероятность допустимой ошибки | ||
| (т-1) | 0,05 | 0,01 | 0,001 |
| 3,84 | 6,64 | 10,83 | |
| 5,99 | 9,21 | 13,82 | |
| 7,81 | 11,34 | 16,27 | |
| 9,49 | 13,28 | 18,46 | |
| 11,07 | 15,09 | 20,52 | |
| 12,59 | 16,81 | 22,46 | |
| 14,07 | 18,48 | 24,32 | |
| 15,51 | 20,09 | 26,12 | |
| 16,92 | 21,67 | 27,88 | |
| 18,31 | 23,21 | 29,59 | |
| 19,68 | 24,72 | 31,26 | |
| 21,03 | 26,05 | 32,91 | |
| 22,36 | 27,69 | 34,53 | |
| 23,68 | 29,14 | 36,12 | |
| 25,00 | 30,58 | 37,70 |
тально подтвердилась: успеваемость значительно улучшилась, и это мы можем утверждать, допуская ошибку, не превышающую 0,001%.
Иногда в психолого-педагогическом эксперименте возникает необходимость сравнить дисперсии двух выборок для того, чтобы решить, различаются ли эти дисперсии между собой. Допустим, что проводится эксперимент, в котором проверяется гипотеза о том, что одна из двух предлагаемых программ или методик обучения обеспечивает одинаково успешное усвоение знаний учащимися с разными способностями, а другая программа или методика этим свойством не обладает. Демонстрацией справедливости такой гипотезы было бы доказательство того, что индивидуальный разброс оценок учащихся по одной программе или методике больше (или меньше), чем индивидуальный разброс оценок по другой программе или методике.
______ Часть II. Введение в научное психологическое исследование____
Подобного рода задачи решаются, в частности, при помощи критерия Фишера. Его формула выглядит следующим образом:
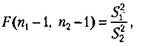
где п1 —■ количество значения признака в первой из сравниваемых выборок; п2 — количество значений признака во второй из сравниваемых выборок; {п1 — 1, п2 — 1) — число степеней свободы; 5f — дисперсия по первой выборке; Si — дисперсия по второй выборке.
Вычисленное с помощью этой формулы значение F-крите-рия сравнивается с табличным (табл. 34), и если оно превосходит табличное для избранной вероятности допустимой ошибки и заданного числа степеней свободы, то делается вывод о том, что гипотеза о различиях в дисперсиях подтверждается. В противоположном случае такая гипотеза отвергается и дисперсии считаются одинаковыми1.
Таблица 34
Граничные значения F-критерия для вероятности допустимой ошибки 0,05 и числа степеней свободы и, и и2
| я, \. | |||||||||
| 9,28 | 9,91 | 9,01 | 8,94 | 8,84 | 8,74 | 8,69 | 8,64 | 8,58 | |
| 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,84 | 5,77 | 5,70 | |
| 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,60 | 4,58 | 4,44 | |
| 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,92 | 3,84 | 3,75 | |
| 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,20 | 3,12 | 3,03 | |
| 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,60 | 2,50 | 2,40 | |
| 3.-24 | 3,0 | 2,85 | 2,74 | 2,59 | 2,42 | 2,33 | 2,24 | 2,13 | |
| 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 2,09 | 1,98 | 1,86 | |
| 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,85 | 1,74 | 1,60 |
1 Если отношение выборочных дисперсий в формуле F-критерия оказывается меньше единицы, то числитель и знаменатель в этой формуле меняют местами и вновь определяют значения критерия.
Глава 3. Статистический анализ экспериментальных данных
Примечание.Таблица для граничных значений ^распределения приведена в сокращенном виде. Полностью ее можно найти в справочниках по математической статистике, в частности в тех, которые даны в списке дополнительной литературы к этой главе.
Пример.Сравним дисперсии следующих двух рядов цифр с целью определения статистически достоверных различий между ними. Первый ряд: 4,6, 5,7,3,4,5,6. Второй ряд: 2,7, 3,6,1,8, 4, 5. Средние значения для двух этих рядов соответственно равны: 5,0 и 4,5. Их дисперсии составляют: 1,5 и 5,25. Частное от деления большей дисперсии на меньшую равно 3,5. Это и есть искомый показатель F. Сравнивая его с табличным граничным значением 3,44, приходим к выводу о том, что дисперсии двух сопоставляемых выборок действительно отличаются друг от друга на уровне значимости более 95% или с вероятностью допустимой ошибки не более 0,05%.
Следующий метод вторичной статистической обработки, посредством которого выясняется связь или прямая зависимость между двумя рядами экспериментальных данных, носит название метод корреляций. Он показывает, каким образом одно явление влияет на другое или связано с ним в своей динамике. Подобного рода зависимости существуют, к примеру, между величинами, находящимися в причинно-следственных связях друг с другом. Если выясняется, что два явления статистически достоверно коррелируют друг с другом и если при этом есть уверенность в том, что одно из них может выступать в качестве причины другого явления, то отсюда определенно следует вывод о наличии между ними причинно-следственной зависимости.
Имеется несколько разновидностей данного метода: линейный, ранговый, парный и множественный. Линейный корреляционный анализ позволяет устанавливать прямые связи между переменными величинами по их абсолютным значениям. Эти связи графически выражаются прямой линией, отсюда название «линейный». Ранговая корреляция определяет зависимость не между абсолютными значениями переменных, а между порядковыми местами, или рангами, занимаемыми ими в упорядоченном по величине ряду. Парный корреляционный анализ включает изучение корреляционных зависимостей только между па-
Часть II. Введение в научное психологическое исследование
рами переменных, а множественный, или многомерный, — между многими переменными одновременно. Распространенной в прикладной статистике формой многомерного корреляционного анализа является факторный анализ.
На рис. 74 в виде множества точек представлены различные виды зависимостей между двумя переменными X и Y (различные поля корреляций между ними).
На фрагменте рис. 74, отмеченном буквой А, точки случайным образом разбросаны по координатной плоскости. Здесь по величине X нельзя делать какие-либо определенные выводы о величине У. Если в данном случае подсчитать коэффициент корреляции, то он будет равен 0, что свидетельствует о том, что достоверная связь между X и У отсутствует (она может отсутствовать и тогда, когда коэффициент корреляции не равен 0, но близок к нему по величине). На фрагменте Б рисунка все точки лежат на одной прямой, и каждому отдельному значению переменной X можно поставить в соответствие одно и только одно значение переменной У, причем, чем большее, тем больше Y. Такая связь между переменными X и У называется прямой, и если это прямая, соответствующая уравнению регрессии, то связанный с ней коэффициент корреляции будет равен +1. (Заметим, что в жизни такие случаи практически не встречаются; коэффициент корреляции почти никогда не достигает величины единицы.)
На фрагменте В рисунка коэффициент корреляции также будет равен единице, но с отрицательным знаком: -1. Это означает обратную зависимость между переменными Xи У, т.е., чем больше одна из них, тем меньше другая.
На фрагменте Г рисунка точки также разбросаны не случайно, они имеют тенденцию группироваться в определенном направлении. Это направление приближенно может быть представлено уравнением прямой регрессии. Такая же особенность, но с противоположным знаком, характерна для фрагмента Д. Соответствующие этим двум фрагментам коэффициенты корреляции приблизительно будут равны +0,50 и -0,30. Заметим, что крутизна графика, или линии регрессии, не оказывает влияния на величину коэффициента корреляции.
Дата добавления: 2015-08-08; просмотров: 1149;
