Силы, возникающие в резьбе
Прямоугольная резьба (Рисунок 103 а).
Гайка, равномерно вращаясь под действием окружной движущей силы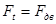 
, приложенной по касательной к окружности среднего диаметра d2, перемещается вверх. При завинчивании она растягивает болт осевой силой 
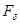.Нужно определить окружную движущую силу Fдв в или Ft.
Считаем, что все силы действуют на один виток, развернем его по среднему диаметру d2, и представим гайку на нем в виде ползуна, на который действуют силы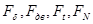 
.
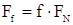сила трения (Рисунок 103 б).
FN - сила нормальной реакции наклонной плоскости. Сложим cилы FN и Ft получим равнодействующую FR.
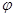- угол трения.
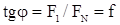
Тангенс угла 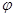равен коэффициенту трения.
Рассмотрим равновесие сил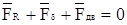 
( Рис. 103в)
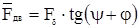
F - окружная, движущая сила. Необходимая для навинчивания гайки на винт с прямоугольной резьбой: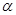 
=0.
Момент сопротивления в прямоугольной резьбе при завинчивании
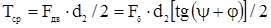
Определим силы трения и установим cooтношения между силами трения в прямоугольной и треугольной резьбах. Для упрощения выводов угол наклона резьбы примем равным нулю: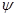 
=0.
В прямоугольной резьбе: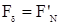 
и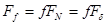 
В остроугольной резьбе: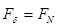 
: 
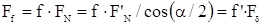или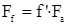 
.
где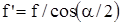 
- приведенный коэффициент трения.
Приведенный угол трения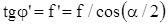 
, т.е. по сравнению с прямоугольной резьбой в треугольной резьбе трение больше, для нормальной метрической резьбы 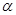= 60° и 
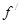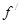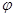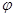=1.15f. Очевидно, что соотношение коэффициентов трения f и соответствует cooтношению между углами трения и ' где 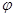'- приведенный угол фения: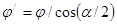 
Окружная сила в остроугольной резьбе: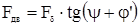 
.
Условие самоторможения в резьбе, при котором статическая осевая сила, растягивающая болт F не вызывает самоотвинчивания гайки:
При свинчивании гайки с болта окружная сила направлена в сторону вращения (Рисунок 104 б).
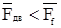- условие самоторможения.
; 
; 
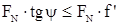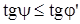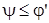
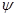- yгол подьема винтовой линии, для метрической резьбы
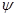=2,4790; 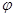'=8040.
Угол подьема должен быть меньше угла трения.
Дата добавления: 2015-08-08; просмотров: 2036;