Поняття про ентропію.

1. Робота теплових машин відбувається за допомогою так званого робочого тіла, в якості якого в переважній більшості випадків використовують речовини в газоподібному (пароподібному) стані. Відомо, що гази володіють здатністю значно змінювати свій об’єм під впливом зовнішніх умов, а це необхідно для роботи теплових машин.

Властивості робочих тіл залежать від того, в яких умовах вони знаходяться. Величини, які характеризують стан робочих тіл, називають параметрами стану. В випадку відсутності зовнішніх силових полів, а також при малому їх впливу на робоче тіло, основними термодинамічними параметрами, які повністю характеризують його стан є: тиск, питомий об’єм (або густина) і абсолютна температура.

Тиск, який позначається літерою 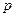, являє собою нормальну складову сили, яка діє на поверхню, віднесену до величини площі цієї поверхні.

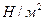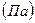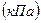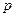В одиницях СІ сила вимірюється в ньютонах, поверхня в квадратних метрах, звідси одиниця виміру тиску – . Ця одиниця отримала назву паскаль . Так як ця одиниця дуже мала, то на практиці використовуються більш крупні кратні одиниці – кілопаскаль або мегапаскаль . Однак слід пам’ятати, що у всі термодинамічні співвідношення, записані в СІ, необхідно підставляти тиск , який виражено в основних одиницях, тобто в паскалях.

Як вже відомо, прилади для виміру тиску, як правило, показують надлишковий тиск, тобто різницю між абсолютним і атмосферним тиском. Параметром стану є тільки абсолютний тиск.

Питомий об’єм, який позначається літерою 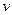, являє собою об’єм одиниці маси речовини, тобто:

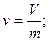
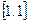
де: 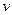- питомий об’єм, м³/кг;

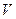- повний об’єм речовини, м³;

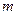- маса речовини, кг.

Зворотна питомому об’єму величина – густина, позначається літерою :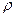

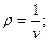
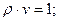
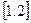
Абсолютна температура, яка позначається літерою 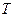, характеризує ступінь нагрітості тіла і вимірюється в кельвінах 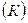. На практиці використовується так звана Міжнародна практична шкала температури, вимірювання в якій звичайно виконують в градусах Цельсія 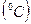. Позначається ця температура літерою .

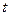Між температурою, яка виражається в кельвінах і в градусах Цельсія, існує наступний зв’язок:

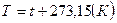
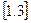
Необхідно пам’ятати, що термодинамічним параметром стану є тільки абсолютна температура .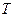

2. Якщо робоче тіло привести в контакт із середовищем, яке має тиск і температуру, відмінні від тиску і температури робочого тіла, то останнє, протягом деякого часу прийде до стану термодинамічної рівноваги із середовищем. При цьому початкові параметри робочого тіла зміняться і приймуть значення, відповідні стану середовища. Вказаний процес зміни стану робочого тіла називається термодинамічним процесом. Розрізняють рівноважні і нерівноважні процеси.

Можна собі уявити, що зовнішні умови (тобто параметри середовища, в якій знаходиться робоче тіло) змінюються із нескінченно малою швидкістю. В цьому випадку термодинамічні параметри робочого тіла встигають не тільки вирівнятись по всьому об’єму робочого тіла, а і прийти в точну відповідність із параметрами зовнішнього середовища. Таким чином, нескінченно повільний процес буде являти собою як би послідовність окремих рівноважних станів робочого тіла із зовнішнім середовищем і може бути охарактеризован як рівноважний термодинамічний процес.

Якщо процес переходу робочого тіла в стан рівноваги із оточуючим середовищем приходить із кінцевою швидкістю, то в кожну мить часу буде спостерігатися відмінність між параметрами середовища і робочого тіла. Відповідно, в такому процесі параметри робочого тіла однозначно не визначаються зовнішніми умовами. Для характеристики стану робочого тіла в нерівноважному процесі необхідно знати додатково хоч би один внутрішній параметр, який характеризує динаміку процесу (наприклад, закон розповсюдження густини, тиску або температури по об’єму робочого тіла). Таким чином, всі процеси, які протікають із кінцевою швидкістю, є нерівноважні і незворотні.

Всі реальні процеси нерівноважні і можуть бути розглянуті як рівноважні тільки із обмеженим ступенем точності. Однак для ряду практично важливих випадків така ідеалізація реальних процесів досить корисна, так як дозволяє отримати порівняно прості математичні залежності для їх опису і аналізу.

Рівноважні процеси володіють важливою властивістю: вони є зворотні, тобто можуть проходити як в прямому, так і в зворотному напрямку через ряд одних і тих самих проміжних станів, не викликаючи ніяких остаточних змін в оточуючому середовищі.

При виконанні незворотних процесів робоче тіло неможливо повернути в початковий стан без деякого додаткового зовнішнього впливу. Таким чином, величина цього додаткового зовнішнього впливу може служити мірою незворотності реальних процесів. Зрозуміло, що ступінь незворотності процесів і причин, які викликають незворотність, необхідно враховувати при виконанні багатьох технічних (реальних) процесів, так як будь який додатковий зовнішній вплив пов’язаний із небажаною витратою додаткової енергії, тобто в кінцевому результаті визначає ступіень бездоганності цих технічних процесів. Причинами, які викликають незворотність нерівноважних процесів, є будь які кінцеві за величиною відхилення робочого тіла від стану рівноваги із оточуючим середовищем, наприклад кінцева різниця тисків (відсутність механічної рівноваги) або кінцева різниця температур (відсутність теплової рівноваги). Тому ясно, що процес нагрівання одного робочого тіла за рахунок іншого, більш гарячого, – процес незворотний, так як передача тепла в зворотному напрямку (від менш нагрітого тіла до більш нагрітого) принципово неможлива без додаткової витрати роботи.

3. Перший закон термодинаміки є частним виразом загального закону збереження і перетворення енергії, який вперше був сформований М.В. Ломоносовим ще в середині XVIII сторіччі.

Для встановлення і доведення закону збереження і перетворення енергії багато зробили такі вчені, як Р. Майер, Гесс, Джоуль, Ленц, Клаузіус, Гельмгольц та ін.

Згідно цього закону енергія не зникає і не виникає знов; енергія може лише переходити із одного виду в інший, і від одного тіла до іншого.

Перший закон термодинаміки встановлює кількісний зв’язок між теплом і роботою при протіканні термодинамічних процесів. Згідно першого закону термодинаміки вся енергія, підведена до робочого тіла у вигляді роботи, може бути відведена від нього у вигляді теплоти, якщо при цьому внутрішня енергія робочого тіла залишиться незмінною. Відповідно, перший закон термодинаміки встановлює закономірність взаємного перетворення тепла і роботи.

Виконаємо аналітичний вираз першого закону термодинаміки.

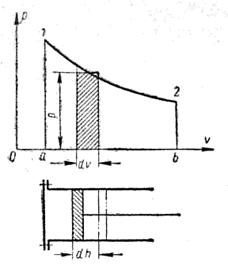
Рисунок 1.1 –Визначення роботи розширення газу.

Нехай в циліндрі із рухомим поршнем знаходиться 1 кг робочого тіла (рисунок 1.1). Якщо до робочого тіла підвести нескінченно малу (елементарну) кількість тепла 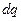, то стан його зміниться і поршень займе нове положення. При цьому зміниться температура, що призведе до зміни внутрішньої енергії на величину 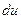. При переміщенні поршня в циліндрі буде виконана робота, пов’язана із зміною об’єму робочого тіла, яка дорівнює .

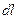Таким чином, внаслідок підведення до робочого тіла теплоти виникле змінення внутрішньої енергії і була виконана робота проти зовнішніх сил.

На основані загального закону збереження енергії можна написати:

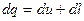
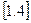
Оскільки , то:

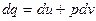
Рівняння 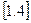і є аналітичним виразом першого закону термодинаміки в диференційній формі. Для кінцевого змінення стан робочого тіла рівняння треба проінтегрувати:

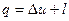
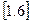
Рівнянню можна надати іншого вигляду, якщо скористатися поняттям ентальпії .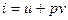

Напишемо диференціал ентальпії:

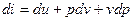
звідси:

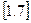
Підставимо рівняння 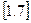в , тоді:

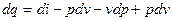
тобто:

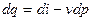
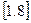
Рівняння 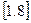також є аналітичним виразом першого закону термодинаміки. Тут член являє собою так звану елементарну корисну, або наявну, роботу.

Для ідеального газу 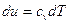і 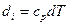, звідси, рівняння і 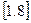можуть бути записані в такій частній формі:

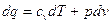
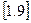
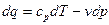
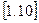
4.Із позиції першого закону термодинаміки допустимі будь які процеси взаємоперетворення тепла і роботи, якщо вони протікають в еквівалентних кількостях. Частина таких процесів може протікати самовільно, тобто без будь якого зовнішнього впливу: наприклад, перетворення механічної роботи в тепло тертя, перехід теплоти від гарячих тіл до холодних. Але здійснення деяких процесів можливе тільки при виконанні додаткових умов, тобто такі процеси не можуть протікати самовільно: наприклад, перехід тепла від холодних тіл до гарячих повинен супроводжуватися обов’язковою затратою додаткової зовнішньої роботи.

Другий закон термодинаміки встановлює напрямок, в якому проходять реальні процеси, і необхідні для їх здійснення умови. Другий закон термодинаміки, як і перший закон, відкрито дослідним шляхом. На відміну від абсолютного першого закону другий закон термодинаміки строго справедливий тільки для систем обмежених розмірів, наприклад Землі і її найближчого оточення; на весь Всесвіт другий закон термодинаміки не може бути розповсюдженим.

Перед тим як сформулювати другий закон термодинаміки, необхідно згадати особливості здійснення колових процесів (циклів). Встановлено, що в прямих циклах (циклах теплових двигунів) підведене від тепловіддатчика до робочого тіла тепло 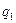неможливо повністю перетворити в корисну роботу, так як частина тепла в кількості 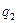обов’язково повинна бути передана від робочого тіла теплоприймачу із більш низькою температурою.

В зворотних циклах (циклах холодильних машин) відведення тепла від менш нагрітих тіл (тепловіддатчиків) до більш нагрітих (теплоприймачам) проходить тільки при умові обов’язковій витраті зовнішньої роботи, яка потім в формі тепла також передається теплоприймачам.

Таким чином, неможна виконати такий періодично діючий тепловий двигун, за допомогою якого можна було б повністю перетворити в роботу все тепло, передане робочому тілу тепловіддатчиком. Це і є одне із формулювань другого закону термодинаміки, який попередньо було сформульовано саме стосовно до закономірностей перетворення тепла в роботу.

Якби вдалося побудувати тепловий двигун, який працює при наявності тільки одного джерела теплоти, тобто враховувати колосальні запаси енергії в оточуючих нас тілах (земна поверхня, вода в морях, океанах і річках), такий двигун практично міг би працювати безмежно довго.

Тому одне із формулювань другого закону термодинаміки стверджує, що неможливо виконати вічний двигун другого роду, тобто двигун, який перетворює повністю в роботу тепло, отримане від єдиного джерела тепла.

В зворотних циклах, тобто в циклах холодильних машин, згідно другого закону термодинаміки відвід тепла від менш нагрітих тіл (тепловіддатчиків) до більш нагрітих (теплоприймачам) можливо виконати тільки при умові обов’язкової витрати зовнішньої роботи, яка потім в формі тепла передається теплоприймачам.

Із сказаного слідує, що другий закон термодинаміки має велике значення для науки і техніки, особливо для енергетики.

5.Залежність дійсної теплоємності газу від температури можна зобразити графічно в координатах 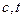(рис. 1.2). На цьому графіку ординати 1-а і 2-b в завданому масштабі представляють значення дійсних теплоємностей при температурах і .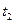

Відомо, що:

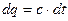
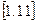
Звідси можна визначити кількість тепла, що підводиться в процесі зміни температури від до 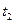. Для цього необхідно проінтегрувати вираз 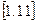в завданому інтервалі температур, тобто:

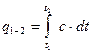
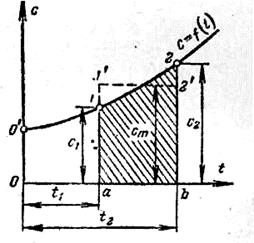
Рисунок 1.2 – Залежність теплоємності від температури

На рисунку 1.2 величина цього інтегралу зображується заштрихованою площиною 1-2-b-a-1 під кривою .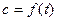

Із рівняння 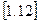слідує, що обчислення кількості тепла за допомогою дійсної теплоємності супроводжується визначеними труднощами. Насамперед, процес інтегрування можливий лише тоді, коли в явному вигляді присутня залежність теплоємності від температури. Але, навіть для ідеального газу ця залежність виходить досить складною. Можна застосувати графічний спосіб визначення кількості теплоти за допомогою графіка 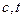. Але в цьому випадку необхідно кожного разу обчислювати площу криволінійної фігури.

Тому, значно зручніше для підрахунку кількості теплоти користуватися величинами середніх теплоємностей, якщо для них складені детальні таблиці. Так, якщо відома середня теплоємність для завданого інтервалу температур, то кількість тепла для 1 кг газу визначається за формулою:

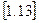
Це рівняння справедливе лише в тих випадках коли температура 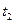> , тобто, коли відбувається нагрівання газу. В противному випадку відбувається охолодження одиниці маси газу.

6.Внутрішня енергія U характеризує енергетичний стан часток які складають робоче тіло. Але для аналізу всіх термодинамічних процесів цього поняття недостатньо, так як потрібен параметр, який характеризує потенційну енергію зв’язків даного робочого тіла із оточуючим середовищем. Таким параметром є ентальпія І:

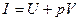
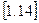
Із аналітичного визначення ентальпії І виходить, що вона складається із внутрішньої енергії U робочого тіла і величини рV, яка являє собою роботу, що витрачається на те, щоб ввести тіло об’ємом V в оточуюче середовище із тиском р.

Ентальпія, як і внутрішня енергія, має в кожному визначеному стані, тобто при визначених параметрах, достатньо конкретне і єдине значення, відповідно, ентальпія є функцією стану, і її зміна в будь якому термодинамічному процесі залежить тільки від параметрів тіла на початку і в кінці процесу і не залежить від характеру (шляху) самого процесу.

Оскільки в технічній термодинаміці приходиться мати справу лише із зміною ентальпії, то відлік її виконується від умовного нуля. Позначається ентальпія для довільної кількості робочого тіла літерою І (Дж), а для 1 кг – літерою і (Дж/кг). Для 1 кг робочого тіла ентальпія дорівнює:

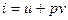
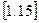
7.Політропними називаються такі процеси, при протіканні яких теплоємність залишається незмінною (с=const).

Відповідно, і всі розглянуті раніше основні процеси можна вважати політропними, якщо в цих процесах буде дотримана постійність теплоємності.

Як відомо, теплоємність ідеальних газів залежить від температури. Відповідно, умова постійності теплоємності в цих процесах є певним припущенням. Але введення поняття політропного процесу дозволяє якісно описати єдиним рівнянням велику групу термодинамічних процесів і провести узагальнюючий аналіз різних властивостей цих процесів. Варто відмітити при цьому, що в двох із розглянутих основних процесів і насправді теплоємність постійна: в ізотермічному процесі, оскільки 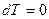, а 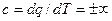, і в адіабатному процесі, так як 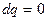, а .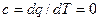

Рівняння політропного процесу може бути виведено із використанням рівняння першого закону термодинаміки. Враховуючи, що в будь якому процесі 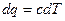, запишемо рівняння 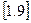і 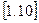таким чином:

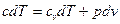
і

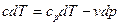
Звідси

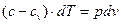
і

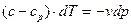
Ділячи почленно перше рівняння на друге, отримаємо:

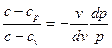
позначимо

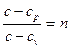
де: 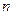- так званий показник політропи.

Тоді:

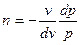
або

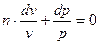
Інтегруючи це рівняння при умові 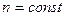, отримаємо:

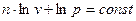
або

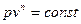
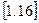
Рівняння 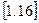і є рівняння політропного процесу в перемінних p i v.

Розглянемо, чому повинен дорівнювати показник політропи в основних процесах при умові протікання їх із постійною теплоємністю:

при 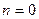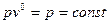- ізобарний процес;

при 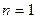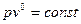- ізотермічний процес;

при 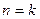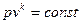- адіабатний процес;

При 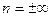рівняння політропи легко перетворюється до наступного вигляду: 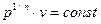. Так як 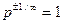, то 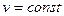- ізохорний процес;

Політропи розширення і стискання в 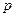, 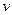- діаграмі при різних значеннях 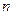приведені на рисунку 1.3. Із розглядання цієї діаграми слідує:

1. всі процеси, що розташовані вище адіабати, протікають із підведенням теплоти;

2. процеси, які розташовані нижче адіабати, протікають із відведенням теплоти;

3. в процесах, які розташовані вище ізотерми, внутрішня енергія збільшується;

4. в процесах, що розташовані нижче ізотерми, внутрішня енергія зменшується;

5. в процесах між адіабатою і ізотермою знаки 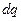і 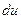різні, а так як знак 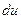відповідає знаку 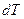, то в цій області теплоємність в процесах буде від’ємною.

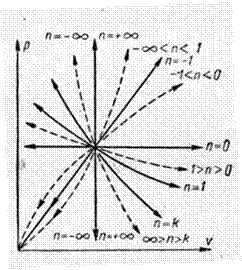
Рисунок 1.3 – Зображення політроп із різними показниками політропи в p, v – діаграмі.

Слід звернути увагу на незвичний вигляд процесів, які протікають при від’ємних значеннях показників політропи. Лінії цих процесів мають вигляд парабол, а не гіпербол, як в процесах із позитивним .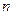

8.Особливе значення в термодинаміці має ще один параметр стану – ентропія, який може бути введений формально, тобто на основі чисто математичних міркувань. Але варто одразу підкреслити, що поняття ентропії має глибокий фізичний зміст, сенс якого буде більш зрозумілим в подальшому, при розгляданні другого закону термодинаміки.

Звернемось знов до розглядання деякого довільного процесу 1 – 2 із ідеальним газом, який зображено на рисунку 1.1. Розіб’ємо весь процес на нескінченно велику кількість елементарних ділянок. На нескінченно малій ділянці кожного процесу підводиться або відводиться нескінченно мала кількість теплоти 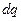при постійній температурі Т. Просумуємо по всьому процесу вирази 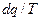взятий в інтервалі від стану 1 до стану 2, тобто 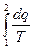. Замінимо величину 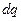під знаком інтегралу на її вираз із рівняння першого закону термодинаміки :

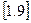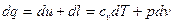
Тоді

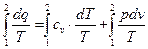
Із рівняння стану ідеального газу слідує, що:

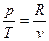
Отримуємо:

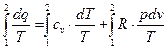
Вважаючи теплоємність 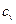сталою, отримаємо:

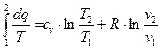
Із розглядання отриманого виразу слідує, що для даного газу величина 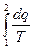залежить лише від зовнішніх параметрів початкового і кінцевого стану ( 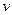і 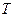) і не залежить від характеру самого процесу. Але раніше на прикладі внутрішньої енергії і ентальпії було показано, що величина, зміна якої не залежить від шляху процесу, є параметром стану.

Відповідно, 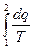являє собою змінення деякого параметру стану. Цей параметр має назву ентропія. Ентропія тіла довільної маси позначається літерою S, а питома, тобто віднесена до 1 кг речовини, - літерою s.

Таким чином, ентропія є величина, зміна якої в будь якому елементарному зворотному термодинамічному процесі дорівнює відношенню тепла 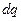, яка бере участь в даному процесі, до абсолютної температури тіла :

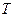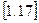
звідси

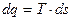
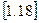
Для кінцевого процесу зміна ентропії буде дорівнювати:

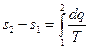
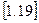
При проведенні теплових розрахунків, як правило, вимагається визначати тільки зміну ентропії, ентальпії і внутрішньої енергії в процесах. Абсолютне значення цих величин при цьому знати не важливо. Тому як для внутрішньої енергії і ентальпії, так і для ентропії обирають умовний початок відліку, при якому її значення приймається рівним нулю. Для ідеального газу прийнято вважати ентропію рівною нулю при нормальних фізичних умовах (н.ф.у.), тобто при t=0 ⁰С і p=101325 Па.

Із формули 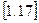витікає, що одиниця виміру питомої ентропії є 1 Дж/(кг×К).

В технічній термодинаміці наряду із 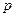, 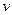- діаграмою широко використовується так звана 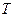, 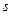- діаграма. В цій діаграмі по вісі ординат відкладаються значення абсолютної температури, а по вісі абсцис – значення ентропії.

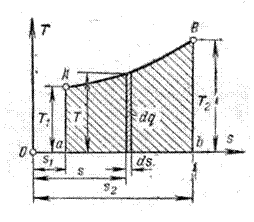
Рисунок 1.4 – Графічне зображення кількості тепла, що передається в процесі, в 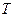, 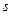- діаграмі.

Розглянемо основні особливості цієї діаграми. Нехай крива АВ (рисунок 1.4) являє собою довільний зворотний процес. Виділимо на цій кривій елементарну ділянку, де зміна ентропії дорівнює . Температуру внаслідок дрібності її змінення на елементарній ділянці процесу можна вважати сталою і рівною 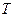. Площадка висотою 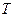і шириною буде являти собою елементарну кількість теплоти 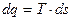. Вся ж площина а-А-В-b-a-q, яка розташована під кривою процесу, дорівнює суммі елементарних площадок або інтегралу від виразу 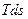, тобто буде дорівнювати теплу, яке бере участь в цьому процесі.

За допомогою 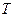, 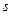- діаграми наочно визначається знак теплоти в процесі.

Так як абсолютна температура Т є завжди величина позитивна, то із виразу 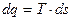витікає, що знак тепла визначається знаком .

Якщо буде від’ємне (процес із убиванням ентропії), то і тепло буде відводитися. В процесах, де буде позитивним (процес із збільшенням ентропії), тепло буде підводитися.

Коротко це можна записати таким чином:

§ якщо 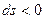, то 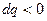(тепло відводиться);

§ якщо 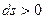, то 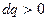(тепло підводиться).

Наприклад, процес АВ, який зображено на рисунку 1.4, буде супроводжуватися підведенням теплоти, так як ентропія в процесі збільшується.