Это уравнение называют уравнением моментов.

Из уравнения моментов (1.5.5), в частности, следует, что если 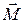= 0, то 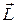=const. Другими словами, если относительно некоторой точки выбранной системы отсчета момент всех сил, действующих на частицу, равен нулю в течение интересующего нас промежутка времени, то относительно этой точки момент импульса частицы остается постоянным в течение этого време­ни.

Ум­ножив обе части этого уравнения на dt, получим d 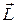= 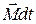— выражение, которое определяет элементарное приращение вектора 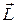. Проинтегрировав это выражение по времени, найдем приращение вектора 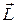за конечный промежуток времени t:

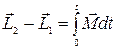(1.5.6)

Величину, стоящую в правой части этого уравнения, назы­вают импульсом момента силы. Таким образом, приращение момента импульса частицы за любой промежуток времени рав­но импульсу момента силы за это же время.