Закон сохранения импульса. Введем понятие замкнутой (или изолирован­ной) системы

Введем понятие замкнутой (или изолирован­ной) системы. Так называют систему частиц, на которую не действуют никакие посторонние тела (или их воздействие пре­небрежимо мало). Другими словами, система замкнута, если внешние силы отсутствуют. Очевидно, что понятие замкнутой системы имеет смысл только по отношению к инерциальным системам отсчета, поскольку в неинерциальных системах от­счета всегда действуют силы инерции, играющие роль внешних сил.

Согласно уравнению (1.4.3), импульс системы может изменя­ться под действием только внешних сил. Внутренние силы не могут изменить импульс системы. Отсюда непосредственно вы­текает закон сохранения импульса:

импульс замкнутой системы частиц остается постоянным, т. е. не меняется со временем:

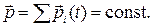(1.4.8)

При этом импульсы отдельных частиц или частей замкнутой системы могут меняться со временем. Однако эти изменения всегда происходят так, что приращение импульса одной части системы равно убыли импульса оставшейся части системы. Другими словами, отдельные части замкнутой системы могут только обмениваться импульсами. Обнаружив в некоторой системе приращение импульса, можно утверждать, что это приращение произошло за счет убыли импульса в окружающих телах.

Импульс может сохраняться и у незамкнутой системы при условии, что результирующая всех внешних сил равна нулю. Это непосредственно вытекает из уравнения (1.4.3). В практическом отношении сохранение импульса в этих случаях представляет особый интерес, ибо дает возможность получать достаточно простым путем ряд сведений о поведении системы, не вникая в детальное рассмотрение процесса.

Кроме того, в незамкнутой системе может сохраняться не сам импульс, а его проекция p_x на некоторое направление X. Это бывает тогда, когда проекция результирующей внешней силы на направление X равна нулю. Действительно, спроецировав уравнение (1.4.3), получим

dp_x/dt = F_{внеш x}, (1.4.9)

откуда следует, что если F_{внеш x} = 0, то p_x = const. Например, при движении системы в однородном поле сил тяжести сохра­няется проекция ее импульса на любое горизонтальное направ­ление, что бы в системе ни происходило.

Необходимо отметить еще один случай, когда закон сохранения импульса можно с большой степенью точности считать справедливым. Так можно поступать, если интервал времени, когда импульс может измениться, мал, и в это время внутренние силы много больше внешних. Указанное справедливо при рассмотрении взрыва, выстрела, соударения.

Подчеркнем еще раз: закон сохранения импульса выполняется только в инерциальных системах, причем, если импульс системы сохраняется в одной инерциальной системе отсчета, то он сохраняется и в любой другой инерциальной системе

Рассуждения, которые привели нас к закону сохранения импульса, целиком опирались на справедливость законов Ньютона. В частности, предполагалось, что материальные точки замкнутой системы взаимодействуют между собой попарно и это взаимодействие подчиняется третьему закону Ньютона. А как обстоит дело в случае систем, не подчиняющихся законам Ньютона, например в системах с электромагнитным излучением?

Ответ на этот вопрос дает опыт, который со всей убедитель­ностью показывает, что закон сохранения импульса оказывает­ся справедливым и для таких систем. Однако в этих случаях в общем балансе импульса необходимо учитывать не только им­пульсы частиц, но и импульс, которым обладает, как выясня­ется в электродинамике, само электромагнитное поле.

Таким образом, опыт показывает, что закон сохранения им­пульса, надлежащим образом, обобщенный, представляет со­бой фундаментальный закон природы, не знающий никаких исключений. Но в таком широком понимании он уже не является следствием законов Ньютона, а должен рассматриваться как самостоятельный общий принцип, являющийся обобщением опытных фактов.