Скорость точки тела, участвующего в сферическом движении
Найдем скорость точки тела, участвующего в сферическом движении. Эта формула носит имя Эйлера.
Вычислим предел отношения малого перемещения точки к малому промежутку времени, в течение которого он происходил при 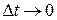 :
:
 .
.
Окончательно

где 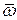 угловая скорость тела относительно мгновенной оси вращения.
угловая скорость тела относительно мгновенной оси вращения.
Используя формулы аналитической геометрии, векторное произведение представим в виде
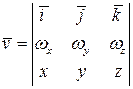 .
.
Раскрыв определитель, получим формулы Эйлера в неподвижной системе координат
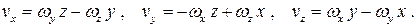
Аналогично можно получить формулы Эйлера в подвижной системе координат, для чего нужно формально произвести в предыдущих соотношениях замену 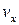 на
на 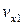 ,
, 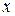 на
на  , и т. д.
, и т. д.
Дата добавления: 2015-08-08; просмотров: 683;
