Угловая скорость, угловое ускорение
 Введём "вектор" малого поворота
Введём "вектор" малого поворота 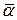 , равный по величине углу поворота
, равный по величине углу поворота 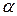 и направленный по оси вращения в такую сторону, чтобы, глядя с его острия видеть вращение происходящим против часовой стрелки. Вектор малого перемещения
и направленный по оси вращения в такую сторону, чтобы, глядя с его острия видеть вращение происходящим против часовой стрелки. Вектор малого перемещения 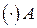 при таком бесконечно малом вращении может быть найден по формуле
при таком бесконечно малом вращении может быть найден по формуле
 .
.
Произведём два последовательных поворота. После первого поворота на угол 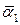 , вектор
, вектор 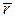 переместится в положение
переместится в положение 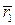
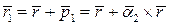 .
.
После второго поворота на угол 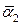 вектор
вектор 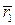 переместится в положение
переместится в положение 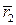
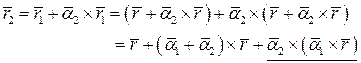
В силу малости 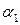 и
и 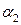 подчёркнутым слагаемым можно пренебречь как величиной более малого порядка, чем остальные компоненты формулы.
подчёркнутым слагаемым можно пренебречь как величиной более малого порядка, чем остальные компоненты формулы.
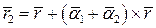 .
.
Но по теореме Эйлера-Даламбера суммарное движение можно записать в виде формулы описывающей один поворот на угол 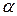 :
:
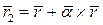 .
.
Сравнивая последние формулы между собой, получим
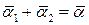 .
.
Т. е. бесконечно малые углы поворота можно считать векторами и складывать по правилу параллелограмма.
Введём определение угловой скорости и углового ускорения:
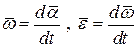 .
.
Угловое ускорение равно линейной скорости конца вектора угловой скорости 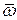 .
.
Т. к. вектор 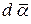 может быть представлен в виде суммы двух или нескольких поворотов
может быть представлен в виде суммы двух или нескольких поворотов
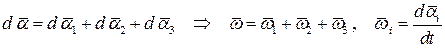
Используя в качестве описанных углов 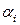 углы Эйлера, получим важную формулу:
углы Эйлера, получим важную формулу:
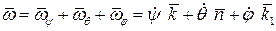 .
.
Дата добавления: 2015-08-08; просмотров: 862;
